किसी चालक की धारिता इसके आकार या आकृति एवं माध्यम पर निर्भर करती है।
C = q/v
चूँकि V = W/q
अत:
C = q2/W
विमा : [M-1 L-2 T4 A2]
गोलाकार चालक की धारिता
R त्रिज्या के धातु के गोले के पृष्ठ पर वितरित आवेश q है जैसे जैसे गोले को आवेशित करते है इसके विभव में वृद्धि होती है।
आवेशित चालक गोले की धारिता C = q/V [समीकरण-1]
गोले के पृष्ठ पर विद्युत विभव –
V = Kq/R [समीकरण-2]
समीकरण-2 से मान समीकरण-1 में रखने पर –
C = R/K
चूँकि K = 1/4πE0
C = R.4πE0
C ∝ R
अत: स्पष्ट है कि गोले की त्रिज्या बढ़ाने पर धारिता बढती है अत: धारिता चालक के आकार पर निर्भर करती है।
धारिता (C) व गोले की त्रिज्या (R) के मध्य सीधी रेखा प्राप्त होती है।
सरल रेखा का ढाल (tanθ) = C/R = 1/K
1/K = नियत
यदि गोले का आकार पृथ्वी के आकार के बराबर हो –
पृथ्वी की त्रिज्या R = 6400 किलोमीटर
C = R.4πE0
C = 711 uF
संधारित्र (capacitor)
संधारित्र एक ऐसी विद्युत युक्त है जिसके आकार में बिना परिवर्तन किये बिना संधारित्र की दोनों प्लेटो पर आवेश का परिमाण समान एवं प्रकृति विपरीत होती है। फलस्वरूप संधारित्र का कुल आवेश शून्य होता है।
किसी संधारित्र की धारिता आवेश को धारण करने की क्षमता होती है।
समान्तर प्लेट संधारित्र में किसी एक प्लेट A पर वितरित आवेश q है यदि इसके समीप समान क्षेत्रफल की समान धातु की दूसरी प्लेट को अल्पदूरी पर रखते है तो प्लेट B की आंतरिक सतह पर -q आवेश व बाहरी सतह पर इतना ही धनावेश आ जाता है। प्लेट B की आन्तरिक सतह पर उपस्थित ऋणावेश के कारण प्लेट A के विभव में जितनी कमी होती है , प्लेट B की बाहरी सतह पर उपस्थित धनावेश के कारण प्लेट A का विभव उतना ही बढ़ जाता है। यदि प्लेट B की बाहरी सतह को भू-सम्पर्कित किया जाए तो मुक्त धनावेश पृथ्वी में चला जाता है फलस्वरूप चालक प्लेट A के विभव में कमी होने से संधारित्र की धारिता बढ़ जाती है। यही संधारित्र का सिद्धांत है।
संधारित्र के प्रकार (types of capacitor)
तीन प्रकार के है –
(i) समान्तर प्लेट संधारित्र
(ii) गोलीय संधारित्र
(iii) बेलनाकार
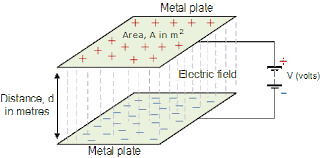
(i) समान्तर प्लेट संधारित्र व इसकी धारिता : समान्तर प्लेट संधारित्र में समान धातु की बनी समान क्षेत्रफल की दो प्लेटे अल्प दूरी पर व्यवस्थित होती है।
प्लेट A पर जितना धनावेश उपस्थित होता है। प्लेट B की आंतरिक सतह पर उतना ही ऋणावेश उपस्थित होता है। प्लेट B की बाहरी सतह को भू-सम्पर्कित रखते है।
संधारित्र की दोनों प्लेटो के मध्य एक समान विद्युत क्षेत्र उत्पन्न होता है।
चालक प्लेट A के कारण प्लेटो के मध्य में स्थित किसी बिंदु पर विद्युत क्षेत्र की तीव्रता –
E1 = σ/2E0 [समीकरण-1]
चूँकि σ = प्लेट का पृष्ठीय आवेश घनत्व चालक प्लेट B के कारण प्लेटो के मध्य में स्थित किसी बिंदु पर विद्युत क्षेत्र की तीव्रता –
E2 = σ/2E0 [समीकरण-2]
बिंदु पर कुल विद्युत क्षेत्र की तीव्रता –
E = E1 + E2
E = σ/2E0 + σ/2E0
E = σ/E0 [समीकरण-3]
यदि संधारित्र की प्लेटो के मध्य की d दूरी में विभवान्तर V हो तो –
विद्युत क्षेत्र की तीव्रता E = V/d = वोल्ट/मीटर (मात्रक) [समीकरण-4]
समीकरण-3 व समीकरण-4 से –
V/d = σ/E0
σ = प्लेट का पृष्ठीय आवेश घनत्व
σ = q/A
A = प्लेटो का क्षेत्रफल
V/d = q/AE0
V = qd/AE0
चूँकि संधारित्र की धारिता –
C = q/V या V = q/C
q/C = qd/AE0
C = AE0/d
प्लेटो का क्षेत्रफल (A) बढ़ाने पर संधारिता की धारिता (C) बढ़ जाती है।
प्लेटो के मध्य की दूरी (d) घटाने पर संधारिता की धारिता (C) बढ़ जाती है।
अत: स्पष्ट है कि समान्तर प्लेट संधारित्र की धारिता प्लेटो के क्षेत्र A के समानुपाती प्लेटो के मध्य की दूरी d के व्युत्क्रमानुपाती होती है।
समान्तर प्लेट संधारित्र की धारिता जब प्लेटो के मध्य पूर्ण रूप से पराविद्युत माध्यम स्थित हो –
यदि समान्तर प्लेट संधारित्र की प्लेटो का क्षेत्रफल A व दोनों प्लेटो के मध्य की दूरी d हो तो निर्वात की स्थिति में संधारित्र की धारिता
C = AE0/d [समीकरण-1]
यदि प्लेटो के मध्य d दूरी में पूर्ण रूप से E0 परावैधुतांक उपस्थित हो तो संधारित्र की धारिता
C’ = A.E/d [समीकरण-2]
चूँकि E = Er.E0 [समीकरण-3]
समीकरण-2 से –
C’ = C.Er
अत: स्पष्ट है कि माध्यम की उपस्थिति में धारिता Er गुना बढ़ जाती है।
समान्तर प्लेट संधारित्र की धारिता जब प्लेटो के मध्य आंशिक रूप से परावैधुत उपस्थित हो –
किसी समान्तर प्लेट संधारित्र की d दूरी पर व्यवस्थित प्लेटो के मध्य t मोटाई का पराविद्युत माध्यम उपस्थित है। पराविद्युत माध्यम को विद्युत क्षेत्र E0 में रखते है तो इसके अणु ध्रुवित हो जाते है। फलस्वरूप पराविद्युत माध्यम की एक सतह ऋणावेशित व दूसरी सतह धनावेशित होने से माध्यम के अन्दर उत्पन्न विद्युत क्षेत्र (Et) बाह्य विद्युत क्षेत्र को कम करने का प्रयास करता है।
समान्तर प्लेट संधारित्र की प्लेटो के मध्य विभवान्तर –
V = V1 + V2
V1 = (d -t) मोटाई अर्थात अर्थात निर्वात में विभवान्तर
V2 = t मोटाई में अर्थात माध्यम में विभवान्तर
C = A.E0/[(d – t) + (t/Er)]