spherical coordinate system in hindi गोलीय निर्देशांक तंत्र क्या है चित्र की सहायता से समझाइये

गोलीय निर्देशांक तंत्र क्या है चित्र की सहायता से समझाइये spherical coordinate system in hindi ?

विशिष्ट लाम्बिक निर्देशांक तंत्र (SPECIAL ORTHOGONAL COORDINATE SYSTEMS)

(i) कार्तीय निर्देशांक तंत्र (Cartesian Coordinate System)

कार्तीय निर्देशांक तंत्र में निर्देशांक पृष्ठे u1 = C1, u2 = C2 तथा u3 = C3 क्रमश: x = C1, y = C2 तथा z = C3 समतल पृष्ठे होती है। यहाँ C1, C2 व C3, नियतांक है। इन तीनों समतल पृष्ठों के युग्मों के प्रतिच्छेदन से तीन सरल रेखायें प्राप्त होती है जिन्हें क्रमश: x, y, z अक्ष कहते हैं। ये तीनों अक्ष परस्पर लम्बवत् होती है तथा मूल बिन्दु O पर परस्पर काटती है। अतः कार्तीय निर्देश तंत्र एक लाम्बिक निर्देशांक तंत्र होता है जैसा कि चित्र (1.6-1) में दर्शाया गया है। इन अक्षों के अनुदिश एकांक सदिश क्रमशः i, j, k द्वारा व्यक्त किये जाते हैं। अतः कार्तीय निर्देशांक तंत्र में,

लाम्बिक वक्र रेखी निर्देशांक तंत्र में किसी बिन्दु का स्थिति सदिश

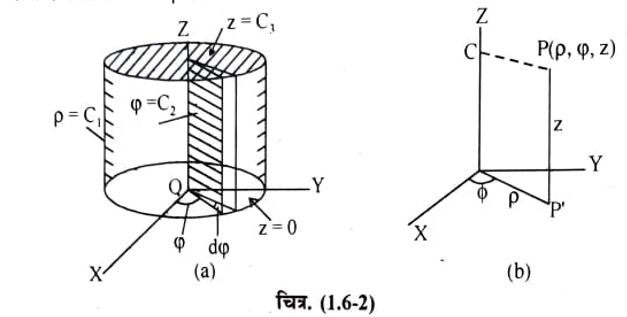
(a)  एक समाक्ष बेलनाकार पृष्ठ होता है जिसकी त्रिज्या p तथा अक्ष z अक्ष होता है।

(b) एक z-अक्ष से पारित अर्ध समतल पृष्ठ होता है तथा x-z तल से p कोण बनाता है।

(c) तल से z = C3 दूरी पर एक समानान्तर वृत्ताकार तल होता है जिसकी त्रिज्या p  होती है।

जब C1 = C2 = C3 = 0 होते हैं तो सभी पृष्ठ बिन्दु O पर मिलते है जिसे बेलनी निर्देशांक तंत्र का मूल बिन्दु O कहते हैं। माना ये तीनों पृष्ठ किसी अन्य बिन्दु P(p, 0, z) पर परस्पर काटते हैं जो बिन्दु P के बेलनी निर्देशांक कहलाते हैं। निर्देशांक वक्रों के आकृति निर्देशांक पृष्ठों की आकृति पर निर्भर करते हैं। चित्र (1.6-2) से स्पष्ट है कि बेलनी पृष्ठ p= C तथा सम के प्रतिच्छेदन से Z अक्ष के समानान्तर सरल रेखा PP प्राप्त होती है। इस रेखा के अनुदिश एकांक सदिश होता है। समतल पृष्ठ = C2 तथा z = C3 के प्रविच्छेदन से CP सरल रेखा प्राप्त होती है। इस सरल रेखा के अनुदिश एकांक सदिश होता है। z = C3 तथा बेलनाकार पृष्ठ p= C के प्रतिच्छेदन से एक वृत्त प्राप्त होता है। बिन्दु P से इस वृत्त पर खींची गई स्पर्श रेखा के अनुदिश एकांक सदिश होता है। इस प्रकार ये तीनों एकांक सदिश परस्पर लम्बवत् दिशा में होते हैं। अतः बेलनी निर्देशांक तंत्र भी एक लाम्बिक निर्देशांक तंत्र होता है। बेलनी निर्देशांक तंत्र में,

चूँकि बेलनी निर्देशांक तंत्र एक लाम्बिक निर्देशांक तंत्र होता है। इसलिए इसके एकांक सदिश अदिश व सदिश गुणनफल के गुणों को सन्तुष्ट करते हैं।

अदिश गुणनफल :

(ii) गोलीय निर्देशांक तंत्र (Spherical coordinate system) 

गोलीय निर्देशांक तंत्र में निर्देशांक पृष्ठों u1 = C1,u2 = C2 तथा u3 = C3 को क्रमशः r = C1, 0 = C2 तथा 0 = C3 द्वारा व्यक्त किया जाता है। यहाँ C1, C2 तथा C3 नियतांक है। इन पृष्ठों की आकृति निम्न प्रकार की होती है।

(a)  एक गोलीय पृष्ठ होता है जिसका त्रिज्या तथा केन्द्र निर्देशांक तंत्र के मूल बिन्दु पर स्थित होता है।

(b) , Z-अक्ष के चारों ओर 0 कोण पर एक शंक्वाकार पृष्ठ होता है जिसका शीर्ष बिन्दु O होता है।

(c) z-अक्ष से पारित एक अर्ध वृत्ताकार समतल होता है जिसका केन्द्र O तथा X-Z तल से ) कोण बनाता है।

जब C1 = C2 = C3 = 0 होते हैं तो सभी पृष्ठ बिन्दु O पर मिलते हैं जिसे गोलीय निर्देशांक तंत्र का मूल बिन्दु O कहते हैं। माना ये तीनों पृष्ठ किसी अन्य बिन्दु P (r, 0, ) पर परस्पर का हैं जो बिन्दु P के गोलीय निर्देशांक कहलाते हैं। निर्देशांक वक्रों की आकृति निर्देशांक पृष्ठों की आकृति पर निर्भर करते हैं। चित्र (1.64) से स्पष्ट है कि गोलीय पृष्ठ r = C1 तथा शंक्वाकार पृष्ठ 0 = C2 का प्रतिच्छेदन r sin 0 त्रिज्या का एक वृत्त बनाता है। बिन्दु P से इस वृत्त पर खींची गई स्पर्श रेखा के अनुदिश एकांक सदिश होता है। शंक्वाकार पृष्ठ 0 = C2 तथा समतल पृष्ठ  = C3 का प्रतिच्छेदन एक सरल रेखा OP बनती है जिसके अनुदिश एकांक सदिश है, होता है। समतल पृष्ठ ¢ = C3 तथा गोलीय पृष्ठ r = C1 का प्रतिच्छेदन r त्रिज्या का एक वृत्त बनाता है। बिन्दु P से इस वृत्त पर खींची गई स्पर्श रेखा के अनुदिश एकांक सदिश होता है। यह तीनों एकांक सदिश परस्पर लम्बवत् होते हैं। अतः गोलीय निर्देशांक तंत्र लाम्बिक निर्देशांक तंत्र होता है। गोलीय निर्देशांक तंत्र में,

चूँकि गोलीय निर्देशांक तंत्र एक लाम्बिक निर्देशांक तंत्र होता है इसलिए इसके एकांक सदिश अदिश व सदिश गुणनफल के गुणों को सन्तुष्ट करते हैं।

स्थिति सदिश एवं विस्थापन

लाम्बिक वक्र रेखी निर्देशांक तंत्र में किसी बिन्दु P का स्थिति सदिश

गोलीय निर्देशांक तंत्र में इसी बिन्दु P का स्थिति सदिश

समीकरण (2) व (3) की तुलना करने पर, स्केल गुणक

तीनों निर्देशांक तंत्रों में परस्पर सम्बन्ध (RELATIONS AMONG ALL THREE COORDINATE SYSTEMS)

(i) कार्तीय निर्देशांक तंत्र से बेलनी निर्देशांक तंत्र में रूपान्तरण (a) स्थिति सदिश (Position vectors ) : माना किसी बिन्दु P के निर्देशांक कार्तीय निर्देशांक तंत्र तथा बेलनी निर्देशांक तंत्र में क्रमश: (x, y, z) तथा (p, 0, z) है जैसा कि चित्र (1.7-1) में दर्शाया गया है। इन निर्देशांकों में संबंध ज्ञात करने के लिए बिन्दु P से X-Y तल पर एक अभिलम्ब PP’ डालते हैं।

(ii) कार्तीय निर्देशांक तंत्र से गोलीय निर्देशांक तंत्र में रूपान्तरण (a) स्थिति सदिश (Position vectors) : माना किसी बिन्दु P के निर्देशांक कार्तीय निर्देशांक तंत्र तथा गोलीय निर्देशांक तंत्र में क्रमश: (x, y, z) तथा (r, 0, ) है जैसा कि चित्र (1.7- 2) में दर्शाया गया है। इन निर्देशांकों में सम्बन्ध ज्ञात करने के लिए बिन्दु P से एक PP’ डालते हैं।