nernst distribution law in hindi नर्नस्ट का वितरण नियम क्या है Limitations सीमाएं

नर्नस्ट का वितरण नियम क्या है Limitations सीमाएं nernst distribution law in hindi ?

नेर्नस्ट वितरण नियम (Nernst Distribution Law)

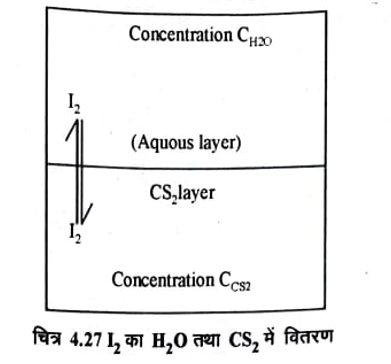
किसी विलेय (ठोस या दव) का दो अमिश्रणीय द्रवों में विभाजन (Distribution of a solut between two nonmiscible solvents):- सन् 1872 में बर्तलों तथा जंग फ्लेश (Berthelot & Jun Fleish) ने प्रयोग कर देखा कि कार्बन टेट्राक्लोराइड या कार्बनडाइ सल्फाइड (CS2) में विभिन्न सान्द्रताओं का बना आयोडीन विलयन आसुत जल के साथ हिलाया जाये और फिर स्थिर छोड़ दिया जाये तो कुछ समय पश्चात मिश्रण दो परतों में विभक्त हो जायेगा।

ऊपरी परत आयोडीन के जलीय विलयन की तथा नीचे की परत आयोडीन के CCI4 या CS2विलयन की होगी (चित्र 4.27) इस प्रकार आयोडीन दोनों परतों में वितरीत होती है और साम्य हो जाता है। अर्थात् आयोडीन अणुओं के जल से CS2 परत में गमन की गति आयोडीन अणुओं के CS2 से जल की परत में गमन की गति के बराबर हो जाती है। साम्यवस्था पर दोनों परतों में आयोडीन की सान्द्रता मानक सोडियम थायोसल्फेट से अनुमापन करके ज्ञात कर लेते हैं। आयोडीन की विभिन्न मात्राऐं लेकर प्रयोग को दोहराते हैं। निश्चित ताप पर यह पाया गया कि दोनों परतों में आयोडीन की सान्द्रताओं का अनुपात स्थिर रहता है तथा यह आयोडीन की कुल . उपस्थित मात्रा पर निर्भर नहीं करता है। अर्थात् आयोडीन की चाहे कितनी मात्रा ही क्यों नहीं ली जाए।

जहाँ K एक स्थिरांक है जिसे वितरण गुणांक (Distribution Coefficient) अथवा विभाजन गुणांक (Partition Coefficient) कहते हैं। इसे विभाजन अनुपात (Distribution Ratio) भी कहते हैं । बर्तेलो तथा जंगफ्लेश ने जो प्रयोग किए वे आंकड़े सारणी 4.13 में दिखाए गए है।

इसी प्रकार जल एवं ईथर के बीच ऑक्सेति अम्ल निकाय में भी उन्होंने वितरण गुणांक के स्थिर मान प्राप्त किए। सन् 1891 में डब्लू नेर्स्ट ने एक नियम प्रतिपादित किया जो उसके नाम पर नेन्सर्ट वितरण नियम (Nernst Distribution Law) कहलाता है। इस नियम के अनुसार-

जब कोई विलेय दो परस्पर सम्पर्क में रखे हुए, अमिश्रणीय द्रवों में वितरित होता है तो, स्थिर ताप एवं साम्य पर दोनों विलायकों में उनकी सान्द्रताओं का अनुपात स्थिर रहता है यदि विलेय दोनों द्रवों के साथ कोई रासायनिक अभिक्रिया नहीं करें अर्थात् विलेय (पदार्थ) दोनों विलायकों में समान आणविक अवस्था में रहें ।

इस प्रकार एक विलेय दो अमिश्रणीय विलायकों A तथा B में स्वयं को वितरित करे तथा समान आणविक स्पीशीज की दोनों विलायक में सान्द्रताऐं CA एवं CB हो तो वितरण नियम के अनुसार-

4.35 गतिक दृष्टिकोण से वितरण नियम की व्युत्पति —– (Derivation of Distribution Law from Kinetic Consideration) विलायकों में विलेय की सान्द्रताएँ क्रमशः CA और CB है। किसी निश्चित ताप पर विलेय की मात्रा के माना कि विलेय स्वयं को दो विलायकों A एवं B में वितरित करता है और साम्यवस्था पर दोनों नहीं होता। वितरण साम्य एक गतिक साम्य है। साम्यवस्था पर विलेय के अण निरन्तर गति कर रहे। लिये CA और CB के मान स्थिर होते हैं। अतः ऐसा प्रतीत होगा कि निकाय विराम पर है। परन्तु ऐसा हैं और समान गति से विलायक A से निकलकर विलायक B में और विलायक B से निकलकर विलायक A में जा रहे हैं। किसी विशेष विलायक में से विलेय के निकलने की गति उस विलायक में उस विलेय की सान्द्रता के समानुपाती होती है।

यही नेन्सर्ट का नियम है।

इसी प्रकार वितरण नियम की ऊष्मागतिकी व्युत्पति भी की जा सकती है।

 वितरण नियम की ऊष्मागतिकी व्युत्पत्ति (Thermodynamic derivation of Distribution Law) माना कि दो अमिश्रणीय द्रव A व B है जो परस्पर सम्पर्क में है और दोनों में एक ही विलेय X विलयन में हैं।

माना कि निश्चित ताप व दाब पर द्रव A में विलेय का रासायनिक विभव व द्रव B में विलेय का रासायनिक विभव H2 है। हम जानते हैं कि

यहाँ U° मानक रासायनिक विभव (अर्थात् रासायनिक विभव जब सक्रियता ईकाई एक हो) तथा पदार्थ की सक्रियता है। 

यहाँ a1 व a2 विलायक A व B में (प्रावस्था I व II में) विलेय की सक्रियता (Activity) है। जब वितरण का साम्य स्थापित हो जाता है तो किसी स्थिर ताप व दाब पर दोनों विलायकों में विलेय के रासायनिक विभवों के मान समान हो जाते हैं। अर्थात्

किसी निश्चित ताप पर किसी पदार्थ का मानक रासायनिक विभव u1° u2° का मान स्थिर होता है चूंकि R भी स्थिरांक है 

यही समीकरण वितरण का सही समीकरण है।

चूँकि विलयन अति तनु है अतः आदर्श विलयन के लिए इनकी सक्रियता का अनुपात लगभग इनकी सान्द्रता (मोल भिन्न, मोलरता या मोललता) के अनुपात के बराबर होती है।

 वितरण नियम की सीमाएं (Limitations of Distribution Law )

वे दशाऐं जिनमें वितरण दृढ़तापूर्वक मान्य है- ऐसा पाया गया कि दो अमिश्रणीय विलायकों में किसी विलेय का वितरण सभी परिस्थितियों में सामान्य वितरण का नियम दृढ़ता से पालन नहीं करता है। अतः यहाँ उन उपयुक्त कारकों का विवेचन करेगें जो इस नियम की उपयुक्तता को सीमित कर देते हैं तथा यह पता लगाऐगें कि किन परिस्थितियों में यह नियम भली-भाँति लागू हो सकता है-

(i) सम्पूर्ण प्रायोगिक निर्धारण के समय ताप स्थिर रहना चाहिए (The temperature should remain constant):- दोनों विलायकों में विलेय की विलेयता ताप पर निर्भर करती है। इसलिए ताप से विलेयता में परिवर्तन दोनों विलायकों में भिन्न हो सकता है। अतः नियम को सही लागू करने के लिए सम्पूर्ण प्रयोग के समय ताप स्थिर रहना चाहिए।

(ii) दोनों विलायकों में विलेय का सान्द्रण यथा सम्भव कम से कम रखना चाहिए अर्थात् विलयन आदर्श रूप में तनु होना चाहिए। (Solution Should be idealy dilute –

सारणी 4.13 से यह देखा गया कि निम्न सान्द्रताओं पर वितरण गुणांक का मान लगभग स्थिर रहता है लेकिन उच्च सान्द्रताओं पर यह लगातार परिवर्तित होता रहता है। अतः यह स्पष्ट है कि सान्द्रता जितनी अधिक होगी नियम से विचलन भी उतना ही अधिक होगा। जैसे-जैसे विलेय की मात्रा बढ़ती जाती है वैसे ही द्रवों की पारस्परिक विलेयता में भी परिवर्तन आता है अतः विलयन की जितनी अधि कि सान्द्रता होगी नियम से विचलन भी उतना ही अधिक होगा।

(iii) विलेय द्वारा विलायकों की परस्पर विलेयता परिवर्तित नहीं होनी चाहिऐ (The Solute should not alter the mutual miscibility of the two solvents)-

वितरण नियम तभी ठीक तरह से लागू हो सकता है जब दोनों विलायक परस्पर अमिश्रणीय हों तथा विलेय की उपस्थिति से इनकी परस्पर विलेयता परिवर्तित नहीं होती हो। विलायकों के थोडे : आपस में विलेय होने पर भी यह नियम लागू हो सकता है। जैसे-जैसे विलेय की मात्रा बढ़ती जाती है, विलायकों की पारस्परिक विलयेता में भी परिवर्तन आता जाता है।

(अ) वितरित पदार्थ पारस्परिक विलेयता को कम कर दें (The distributed solute lowers the mutual solubilities)-

इस स्थिति में यदि हम विलेय की मात्रा बढ़ाते चले तो विलायकों की पारस्परिक विलेयता कम · होती जाएगी और अन्ततः शून्य हो जायेगी। इस स्थिति में वितरण अनुपात शुद्ध विलायकों में विलयेताओं के अनुपात के बराबर हों जायेगा। अतः

जहाँ S1 व S2 विलेय की दोनों विलायकों में विलेयता है।

(ब) वितरण पदार्थ पारस्परिक विलेयता को बढ़ा दे (The mutual soubility is raised)- इस स्थिति में विलेय की मात्रा बढ़ाने पर विलायकों की पारस्परिक विलेयता बढ़ती जाती है तथा विलेय की बढ़ी हुई मात्रा दोनों प्रावस्थाओं को समान कर देती है जिससे दोनों परस्पर मिश्रित हो जाते हैं। इस प्रकार वितरण अनुपात लगातार परिवर्तित होता हुआ अन्त में एक हो जायेगा। उदाहरणार्थ- मैलोनिक अम्ल के जल व ईथर के वितरण में मेलोनिक अम्ल की मात्रा बढ़ाने पर इस प्रकार की घटना देखी गई।

(स) पारस्परिक विलेयता अनियमित रूप से बदलती है- यदि एक द्रव की दूसरे द्रव में विलेयता बढ़ जाये तथा दूसरे द्रव की पहले द्रव में विलेयता कम हो जाये तो ऐसी दशा में वितरण गुणांक भी बदल जायेगा।

(iv) दोनों विलायकों में विलेय समान आणविक अवस्थाओं में रहना चाहिए

(The Solute must remain in the same molecular state in both the Solvents):-

डब्लू नेर्स्ट ने ज्ञात किया कि C1/C2 का मान स्थिरांक के बराबर तभी होता है जब दोनों विलायकों

में विलेय पदार्थ अपनी अवस्था नहीं बदलता है अर्थात् समान आणविक अवस्थाओं में रहता है। लेकिन ऐसा बहुत कम होता है। प्रायः यह देखा गया है कि विलेय के अणुओं का दोनों अथवा किसी एक विलायक में संगुणन (Association), वियोजन ( Dissociation) या विलायक संकरण ( Solvation) हो जाता है जिससे विलेय की आणविक अवस्था परिवर्तित होती है और वितरण गुणांक स्थिर नहीं रहता है। इन अवस्थाओं में वितरण नियम में संशोधन करना पड़ता है। उदाहरणार्थ-

 विलेय का एक प्रावस्था में संगुणन (The solute is associated in one of the solvents)

माना कि विलेय X, प्रावस्था I में सामान्य अणु रहता है जबकि प्रावस्था II में निम्न समीकरण के अनुसार संगुणन हो जाता हो तथा संगुणित होकर संकर स्पीशीज Xn बनाता है।

nX ⇒ Xn

माना कि प्रावस्था I में विलेय के असंगुणित अणुओं का सान्द्रण C तथा प्रावस्था II में संगुणित तथा सामान्य अणुओं की सान्द्रताऐं क्रमश: C2 तथा C3 है (चित्र 4.28) । दोनों प्रावस्थाओं में समान आणविक स्पीशीज अर्थात् असंगुणित अणुओं के लिए वितरण नियम के अनुसार-

C1/C3 = K (वितरण स्थिरांक) ……………………..(26)

प्रावस्था II में संगुणन प्रक्रम पर द्रव्य अनुपाती क्रिया के नियमानुसार,

अतः इस प्रकार के उदाहरणों के लिए समीकरण ( 28 ) का प्रयोग करने पर K पर मान स्थिर आयेगा। समीकरण (28) का उपयोग किसी विलायक के अन्दर विलेय के अणुओं की संगुणन संख्या n ज्ञात करने में किया जाता है। बेन्जोइक अम्ल का जल तथा बेन्जीन में वितरण इसी प्रकार का उदाहरण है जिसके परिणाम सारणी 4.14 में दिए गए है।

उपर्युक्त सारणी में दिये गए मानों से स्पष्ट है कि C1/C2 अनुपात परिवर्तित होता है। जबकि C1/C2का मान स्थिर रहता है। इससे सिद्ध होता है कि बेन्जोइक अम्ल बेन्जीन में द्विगुणित अणुओ (n = 2) (Dimer) अर्थात् (C6H5COOH)2 के रूप में रहता है।

 विलेय का एक विलायक में वियोजन (The Solute is dissociated in one of the solvents)

माना कि विलेय XY विलायक प्रावस्था I में सामान्य रहता है तथा विलायक प्रावस्था II में X तथा Y स्पिशीज में वियोजित हो जाता है। (चित्र 4.29) ।

माना कि विलेय की प्रावस्था II में वियोजन की मात्रा a है । प्रावस्था I में सान्द्रता C1 तथा प्रावस्था II में सान्द्रता C2 है। प्रावस्था II में अवियोजित अणुओं की सान्द्रता C2 (1 – x ) होगी ।

वितरण नियम दोनों विलायकों में उपस्थित समान आणविक स्पीशीज अर्थात् अवियोजित अणुओं पर ही लागू होता है। अतः वितरण नियम के अनुसार-

करते हैं। यह स्थिति प्रायः कार्बनिक अम्लों में पायी जाती है जबकि वे जल तथा कार्बनिक विलायको जब दोनों प्रावस्थाओं में से किसी एक में वियोजन होता है तो संशोधित समीकरण (29) का प्रयोग में वितरित होते हैं। इसी प्रकार अगर विलेय दोनों विलायकों में वियोजित हो तो वितरण का नियम निम्नानुसार होगा।

जहाँ a1 व a2 विलेय की क्रमशः विलायक A व B में वियोजन की मात्रा है।

 विलेय का किसी एक विलायक के साथ संयोग या विलायक संकरण का बनना (The Solute gets solvated in one of the solvents)

जब विलेय किसी एक विलायक के साथ रासायनिक संयोग करता है तो वितरण समीकरण उसी रूप में ही प्रयुक्त होती है केवल K के मान में सांख्यिकी परिवर्तन आ जाता है।

मान लीजिए कि विलेय X विलायक I में सामान्य अणुओं के रूप में तथा विलायक II में विलायक संकरित अणुओं के रूप में निम्न समीकरण के अनुसार रहता है।

जैसा कि चित्र 4.30 में दर्शाया गया है। साम्यवस्था में प्रावस्था I में वितरित अणुओं की सान्द्रता C तथा प्रावस्था II में सामान्य अणुओं तथा विलायक संकरित अणुओं की सान्द्रताऐं क्रमश: C2 तथा C3 है । माना कि प्रावस्था II में विलायक के अणुओं की सान्द्रता Cs है |

वितरण के अनुसार

C1/C2  =K …………………….(30)

प्रावस्था II में निम्नलिखित साम्यावस्था रहती है।

उपर्युक्त साम्यावस्था पर द्रव अनुपाती क्रिया का नियम लागू करने पर

चूँकि प्रावस्था II में विलायक की सान्द्रता Cs अन्य सान्द्रताओं से बहुत अधिक है, अतः इसे विलेय से विलायक संकरण बनने पर भी स्थिर माना जा सकता है। अतः समीकरण ( 31 ) को निम्न प्रकार लिखा जा सकता है-

(C2+ C3) प्रावस्था II में विलेय का कुल सान्द्रण है। समीकरण (34) से स्पष्ट है कि विलायकों में से किसी एक से विलेय का विलायक संकरण बनने पर भी वितरण की मौलिक समीकरण में कोई अन्तर नहीं आता केवल K का सांख्यिकीय मान बदल जाता है ।