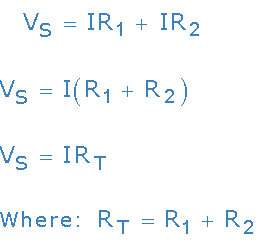Kirchhoff’s law in hindi किरचॉफ का प्रथम नियम , द्वितीय नियम किरचॉफ के नियम : हमने ओम का नियम पढ़ा है जिसकी सहायता से परिपथ में प्रवाहित धारा , विभवान्तर इत्यादि का अध्ययन किया जाता है।
लेकिन
ओम का नियम सरल परिपथों के लिए ही उपयोगी है। जटिल परिपथों को हल करने के लिए ओम के नियम से कठिनाई हो जाती है।
अतः जटिल परिपथों को हल करने के लिए किरचॉफ ने दो नियम दिए इन्हे किरचॉफ के नियम कहते है।
हम इन दोनों नियमों को विस्तार से पढ़ेंगे उससे पहले इससे सम्बन्धित कुछ परिभाषाएं पढ़ लेते है।
संधि : विद्युत परिपथ का वह बिंदु जहाँ तीन या तीन से अधिक शाखाएँ मिलती है उसे संधि कहते है।
शाखा : परिपथ का वह भाग जिसमे धारा का मान नियत रहता है शाखा कहलाती है।
लूप : प्रतिरोधों , चालकों इत्यादि से बने बंद परिपथ को लूप कहते है।
किरचॉफ का प्रथम नियम (Kirchhoff’s first law)
किरचॉफ़ का पहला नियम संधि नियम भी कहलाता है , क्यूंकि यह सन्धि से सम्बन्धित है। इस नियम के अनुसार
“किसी वैद्युत परिपथ में किसी सन्धि पर मिलने वाली सभी धाराओं का बीजगणितीय योग शून्य होता है “
अर्थात
∑I = 0
इस नियम को हम इस प्रकार भी कह सकते है
” विद्युत परिपथ में किसी संधि पर प्रवेश करने वाली धारा का योग , उसी संधि से निकलने वाली धारा के योग के बराबर होता है “
किसी संधि पर आने वाली धाराओं का योग = उसी संधि से जाने वाली धाराओं का योग
इसे किरचॉफ का प्रथम नियम कहते है।
यह नियम
आवेश संरक्षण के नियम पर आधारित है इसलिए तो संधि पर आने वाली धारा अर्थात आने वाला आवेश जाने वाले
आवेश के बराबर होता है।
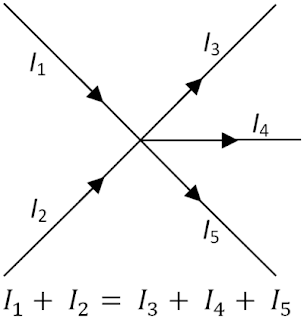
चित्र को ध्यान से देखिये इसमें किसी संधि से 5 धाराएं सम्बन्धित दिखाई गयी है। इनमे से
I1 व I2 धाराएं संधि में प्रवेश कर रही है जबकि I3 , I4 ,I4 धाराएं संधि से बाहर निकल रही है।
किरचॉफ़ के नियम से
संधि पर प्रवेश करने वाली धाराओं का योग = संधि से निकलने वाली धाराओं का योग
अतः
किरचॉफ का द्वितीय नियम (Kirchhoff’s second law)
किरचॉफ के दूसरे नियम को लूप का नियम भी कहते है क्यूंकि यह लूप से सम्बंधित है। इस नियम के अनुसार
” किसी बंद परिपथ या लूप में परिपथ का परिणामी
विद्युत वाहक बल , परिपथ के सभी अवयवों के सिरों पर उत्पन्न विभवांतरों के योग के बराबर होता है “
या
” बंद परिपथ या लूप मे प्रतिरोधों के सिरों पर उत्पन्न
विभवांतर का बीजगणितीय योग उस परिपथ में स्थित सेलो के विद्युत वाहक बालो के बीजगणितीय योग के बराबर होता है।
∑IR = ∑ε
इस समीकरण को किसी परिपथ में लागू करने के लिए चिन्हों का ध्यान रखना पड़ता है ये निम्न है
1. परिपथ में
विद्युत धारा की दिशा में चलने पर प्रतिरोध के सिरों पर विभवांतर का मान धनात्मक लेते है तथा धारा के विपरीत दिशा में चलने पर प्रतिरोध के सिरों पर विभवांतर ऋणात्मक लेते है।
2. परिपथ में विद्युत धारा की दिशा में चलने पर रास्ते में सेल के ऋण सिरे से धन सिरे की ओर चलने पर विधुत वाहक बल धनात्मक लेते है तथा सेल के धन सिरे से ऋण सिरे की ओर चलने पर विद्युत वाहक बल को ऋणात्मक लेते है।
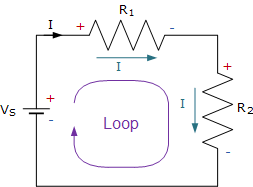
हमें निम्न लूप के लिए किरचॉफ का नियम उपयोग लेते हुई समीकरण लिखकर हल करना है
R1 प्रतिरोध के सिरों पर उत्पन्न विभवांतर = IR1
R2 प्रतिरोध के सिरों पर उत्पन्न विभवांतर = IR2
चिन्हों का ध्यान का ध्यान रखते हुए विभवांतर IR1 तथा IR2 को धनात्मक लेते है तथा सेल में ऋण टर्मिनल से धन टर्मिनल की तरफ चला जा रहा है अतः सेल का विद्युत वाहक बल भी धनात्मक होगा
अतः
किरचॉफ के द्वितीय नियम से
प्रतिरोधों के सिरों पर उत्पन्न विभवांतर का बीजगणितीय योग = सेलो के विद्युत वाहक बालो के बीजगणितीय योग
अतः
इसे आवश्यकतानुसार आगे भी निम्न प्रकार हल किया जा सकता है और हर मान ज्ञात किया जा सकता है।
Sbistudy
