असमान चुम्बकीय क्षेत्र में नियत वेग से गति के कारण आयताकार लूप में प्रेरित वि.वा.बल एवं धारा Induced e.m.f and current in a rectangular loop

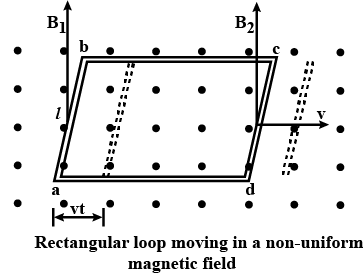
SbistudyMarch 11, 2018May 7, 2024inPhysics

Induced e.m.f and current in a rectangular loop moving in a non uniform magnetic field in hindi असमान चुम्बकीय क्षेत्र में नियत वेग से गति के कारण आयताकार लूप में प्रेरित वि.वा.बल एवं धारा : माना एक आयताकार आकृति है जिसे चित्र में abcd से दर्शाया गया है , यह एक असमान चुम्बकीय क्षेत्र में रखी हुई है। यहाँ असमान से तात्पर्य है की चुम्बकीय क्षेत्र का मान अलग अलग जगह पर भिन्न है।

मान लेते है की आयताकार आकृति (कुण्डली) की ab भुजा पर चुंबकीय क्षेत्र का मान B₁ है तथा cd भुजा पर चुम्बकीय क्षेत्र का मान B₂ है।

इस आयताकार कुण्डली को इस प्रकार रखा जाता है की यह चुम्बकीय क्षेत्र के लम्बवत रहे , अब इस आयताकार कुंडली को v वेग से इस प्रकार गति कराते है की इसकी भुजा ab तथा cd के लम्बवत दिशा में गति हो।

यहाँ भुजा ab व cd की लम्बाई l है , अगर यह कुण्डली t समय तक गति करती है तो , t समय में तय की गयी

दूरी = vt

तथा t समय में पार किया गया क्षेत्रफल = lvt

हमने पहले ही बात की है की ab भुजा पर चुंबकीय क्षेत्र का मान B₁ है तथा cd भुजा पर चुम्बकीय क्षेत्र का मान B₂ है।

तथा जितना क्षेत्रफल कुण्डली ab की तरफ खिसकी है उतना ही cd की तरफ खिसकी है अत: हम कह सकते है की कुण्डली का जितना क्षेत्रफल(A) B₁चुंबकीय क्षेत्र से निकलता है उतना ही क्षेत्रफल(A) B₂चुंबकीय क्षेत्र में प्रवेश करता है।

B₁चुंबकीय क्षेत्र से निकलने में चुम्बकीय फ्लक्स में कमी

ϴ_B1 = B₁A = B₁lvt

B₂चुंबकीय क्षेत्र में प्रवेश करने से फ्लक्स में वृद्धि

ϴ_B2 = B₂A = B₂lvt

अतः A पार करने में कुण्डली के फ्लक्स में आया परिवर्तन

△ϴ = ϴ_B2 – ϴ_B1= B₂lvt – B₁lvt

t को दूसरी तरफ लाने पर

△ϴ/t = B₂lv – B₁lv

△ϴ/t = (B₂ – B₁)lv

फैराडे के अनुसार प्रेरित विद्युत वाहक बल

e = △ϴ/t

इसका मान हम ज्ञात कर चुके है अतः