WhatsApp Group Join Now

Telegram Join Join Now

Download our app now हमारी app डाउनलोड करे

प्रथम कोटि की अभिक्रिया का समाकलित वेग समीकरण तथा अर्द्ध आयुकाल

First order reaction (प्रथम कोटि की अभिक्रिया) velocity equation and half time with examples and question answers velocity equation and half time with examples

प्रथम कोटि की अभिक्रिया का समाकलित वेग समीकरण :

सब्सक्राइब करे youtube चैनल

जब किसी अभिक्रिया का वेग क्रियाकरको की सांद्रता के प्रथम घात के समानुपाती होता है। तो इसे प्रथम कोटि की अभिक्रिया कहते है।

माना एक अभिक्रिया निम्न है।

R → उत्पाद

माना प्रारम्भ में अर्थात t = 0 समय पर क्रियाकारक की प्रारंभिक सांद्रता[R]₀है t समय पश्चात इसकी सांद्रता [R] है।

अभिक्रिया वेग∝[R]

= – d[R]/dt = k[R]

यहाँ k प्रथम कोटि की अभिक्रिया का वेग स्थिरांक है। उपरोक्त समीकरण को प्रथम कोटि की अभिक्रिया का अवकल वेग समीकरण कहते है।

या

– d[R]/[R] = k dt

– (माइनस) से गुणा करने पर

d[R]/[R] = – k dt

समाकलन करने पर

∫d[R]/[R]=∫– k dt

ln[R] = -kt + I .. . . . . . . . . समीकरण 1

यहाँ I समाकलन नियतांक है इसका मान निम्न प्रकार से ज्ञात करते है।

यदि t = 0 है तो[R] =[R]₀होगा।

अतः

समीकरण 1 से

ln[R] = -kt + ln[R]₀

kt =ln[R]₀–ln[R]

kt =ln[R]_0 /[R]

kt = 2.303 log[R]_0 /[R]

k= (2.303/t) log[R]_0 /[R]

यह प्रथम कोटि की अभिक्रिया का समाकलित वेग समीकरण कहलाता है।

प्रथम कोटि की अभिक्रिया का अर्द्ध आयुकाल ज्ञात करना :

प्रथम कोटि की अभिक्रिया के लिए

k= (2.303/t) log[R]_0 /[R]

या

t= (2.303/k) log[R]_0 /[R]

यदि t =t_1/2है तो [R] =[R]₀/2 होगा।

t_1/2=(2.303/k) log ([R]₀)_/([R]₀/2)

t_1/2=(2.303/k) log 2

चूँकिlog 2 = 0.3010

log 2 का मान रखने पर

t_1/2=(2.303/k) x0.3010

t_1/2= 0.693/k

अतः प्रथम कोटि की अभिक्रिया का अर्द्धकाल क्रियाकरको की प्रारंभिक सांद्रता पर निर्भर नहीं करता।

प्रश्न 1 : प्रथम कोटि की अभिक्रिया के लिए अर्द्ध आयुकाल ज्ञात करो यदि वेग स्थिरांक

(1) 200sec^-1

(2) 2Min^-1

(3) 4Year^-1

उत्तर : (1) t_1/2= 0.693/k

t_1/2= 0.693/2 x10^-2

t_1/2= 3.465x10^-3sec

(2) t_1/2= 0.693/k

t_1/2= 0.693/2

t_1/2= 3.465x10^-1Min

(3)t_1/2= 0.693/k

t_1/2= 0.693/ 4

t_1/2= 1.732x10^-1Year

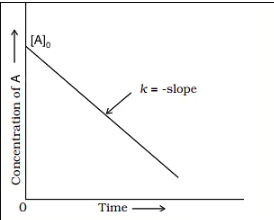
प्रथम कोटि की अभिक्रिया का आलेख निरूपण :

(1)प्रथम कोटि की अभिक्रिया के वेग समीकरण से

ln[R] = – kt + ln[R]₀

_{y = -mx + c (अन्तः खण्ड)}

(2)प्रथम कोटि की अभिक्रिया के वेग समीकरण से

kt =ln[R]_0 /[R]

kt = 2.303 log[R]_0 /[R]

log[R]_0 /[R] =kt /2.303

Concentration v Time Graphs

प्रश्न : प्रथम कोटि की अभिक्रिया का वेग स्थिरांक 60sec^-1है। क्रियाकारक की प्रारंभिक सांद्रता से 1/16 भाग रह जाने में कितना समय लगता है।

उत्तर : t = (2.303/k) log [R]_0 /[R]

दिया गया है

k = 60 sec^-1

[R]₀= 1

[R] = 1/16

t = ?

t = (2.303/60) log 1 /(1/16 )

t = (2.303/60) log 16

t = 46.5 x 10^-3

प्रथम कोटि की अभिक्रिया में 99% अभिक्रिया पूर्ण होने में लगा समय 90% अभिक्रिया पूर्ण होने में लगने वाले समय से दोगुना होता है , सिद्ध कीजिये।

उत्तर :

t_99%पूर्ण होने में लगा समय

t = (2.303/k) log [R]_0 /[R]

t_99%= ?

[R]₀= 100

[R] = 1

t_99%= (2.303/k) log₁₀₀

_{t99% = (2.303/k) x 2 [log 100 = 2 ]}

_{t90% पूर्ण होने में लगा समय}

_{t = (2.303/k) log [R]0 / [R]}

t_90%= ?

[R]₀= 100

[R] = 10

t_90%= (2.303/k) log_100/10

_{t90% = (2.303/k) [log 10 = 1 ]}

_t99%/t_90%= [(2.303/k) x 2] / (2.303/k)

_t99%/t_90%= 2

t_99%= 2 x t_90%

_{प्रथम कोटि की अभिक्रिया का समाकलित वेग समीकरण निम्न है}

k = (2.303/t) log [R]_0 /[R]

उपरोक्त समीकरण को निम्न प्रकार से भी व्यक्त कर सकते है।

माना t = 0 समय पर अर्थात प्रारम्भ में क्रिया कारकों की प्रारंभिक सांद्रता a molL^-1है। t समय पश्चात इसका x मोल वियोजित हो जाता है तो t समय पश्चात् इसकी शेष बची मात्रा (a – x) होगी अतः

[R]₀= a

[R] = (a – x)

k = (2.303/t) log_a /(a – x)

प्रथम कोटि की अभिक्रिया के उदाहरण

(1) रेडियोएक्टिव पदार्थ का विघटन :

++Nuclear+Equations+Nuclear+Equations

λ = (2.303/t)log(N₀/N_t)

यहाँλ = विघटन स्थिरांक

N₀= रेडियो ऐक्टिव तत्व की प्रारंभिक मात्रा

N_t= T समय पश्चात रेडियो सक्रिय तत्व की बची मात्रा

उदाहरण 2 : एथिल ऐसिटेट का अम्लीय माध्यम में जल अपघटन :

CH₃COOC₂H₅ + H₂O = C₂H₅OH+ CH₃COOH

अभिक्रिया वेग ∝ (CH₃COOC₂H₅)(H₂O)

उपरोक्त क्रिया में जल को अधिक मात्रा में लिया जाता है। क्रिया के बाद जल की सांद्रता में कोई मापने योग्य परिवर्तन नहीं होता अतः जल की सान्द्रता को स्थिर मान सकते है।

अतः

अभिक्रिया वेग ∝ (CH₃COOC₂H₅)

उपरोक्त समीकरण से स्पष्ट है की अभिक्रिया वेग ऐथिल ऐसिटेट की सांद्रता के प्रथम धातु के समानुपाती है अतः यह प्रथम कोटि की अभिक्रिया है।

नोट : इस अभिक्रिया की कोटि एक तथा अणुसंख्यता या आणविकता दो है अतः इसे छदम प्रथम कोटि या छ्दम एकाणुकता अभिक्रिया कहते है।

उदाहरण : C₁₂H₂₂O₁₁(sucrose) + H₂O= C₆H₁₂O₆(glucose) + C₆H₁₂O₆(fructose)

उपरोक्त अभिक्रिया कोटि एक व आणविकता दो होगा अतः यह छदम एकाणु अभिक्रिया है।

प्रोयोगिक वेग ∝ (C₁₂H₂₂O₁₁)