entropy in hindi in thermodynamics definition एन्ट्रॉपी की परिभाषा लिखिए परिभाषा क्या है

एन्ट्रॉपी की परिभाषा लिखिए परिभाषा क्या है entropy in hindi in thermodynamics definition ?

एन्ट्रोपी (Entropy)

ऊष्मागतिकी के द्वितीय नियम के अध्ययन के बाद एक ऐसे फलन की आवश्यकता अनुभव की गई जिसका प्रक्रमों की कसौटी के रूप में उपयोग किया जा सके। यह फलन भी अवस्था फलन होना चाहिये अर्थात् इसका मान तंत्र की अवस्था पर निर्भर करे न कि प्रक्रम के पथ पर इस फलन को एन्ट्रोपी कहा गया। इसे S द्वारा व्यक्त करते है, परन्तु इसकी परिभाषा इसमें अनन्त सूक्ष्म परिवर्तन ds के रूप में दी जाती है ।

किसी तंत्र द्वारा उत्क्रमणीय प्रकार से अवशोषित ऊष्मा तथा वह परमताप जिस पर ऊष्मा अवशोषित की गई है का अनुपात एन्ट्रोपी परिवर्तन (Entropy change) कहलाता है। यदि T ताप पर dqrev उत्क्रमणीय प्रकार से अवशोषित ऊष्मा की मात्रा हो तो

यदि तंत्र निश्चित ताप T पर qrev ऊष्मा अवशोषित करके A अवस्था से B अवस्था में जाता है तो एन्ट्रोपी में एक परिमित (Finite ) परिवर्तन होता है जो कि निम्न प्रकार प्रदर्शित किया जा सकता है।

ऊर्जा के समान ही एन्ट्रोपी एक अवस्था फलन है, अतः dS, dE के समान यथातथ अवकल (Exact differential) होता है तथा उसे ऊष्मागतिकी चरांको (P, V, T) के रूप में व्यक्त किया जा सकता है एन्ट्रोपी का मान तंत्र में उपस्थित द्रव्य की मात्रा पर निर्भर करता है अतः एन्ट्रोपी एक मात्रात्मक गुण (Extensive Property) है। एन्ट्रोपी की इकाई कैलोरी प्रति डिग्री (Cal deg -1 ) या जूल प्रति डिग्री (JK – 1) है । इसे कभी – कभी एन्ट्रोपी इकाई ( Entropy unit, e.u.) में भी व्यक्त किया जाता है। चूंकि एन्ट्रोपी मात्रात्मक गुण है, अतः एक मोल पदार्थ के लिये एन्ट्रोपी की इकाई कैलोरी प्रति डिग्री प्रतिमोल (Cal deg-1 mole-1) या जूल प्रति डिग्री प्रति मोल JK – 1 mole-1 होती है। यह एन्ट्रोपी मोलर एन्ट्रोपी कहलाती है।

एन्ट्रोपी की धारणा का गणितीय निरूपण (Mathematical Formulation of Concept of Entropy)

कान इंजन की दक्षता की समीकरण (16) द्वारा

उपरोक्त समीकरण में q2अवशोषित ऊष्मा है धनात्मक चिन्ह तथा १ विसर्जित ऊष्मा है जिसे ऋणात्मक चिन्ह दिया गया है। यदि q तथा 2 को ऊष्मा विनिमय के रूप में ही माना जाये अर्थात अवशोषण विसर्जन कुछ भी हो सकता है। अतः उपरोक्त समीकरण को इस प्रकार भी लिखा जा सकता है।

चूंकि समीकरण (37) में एक पद समतापी उत्क्रमणीय प्रक्रम तथा दूसरा रूद्धोष्म उत्क्रमणीय प्रक्रम से सम्बन्धित है अतः यह कह सकते हैं कि पदों का बीजीय संकलन (Algebric Summation) शून्य

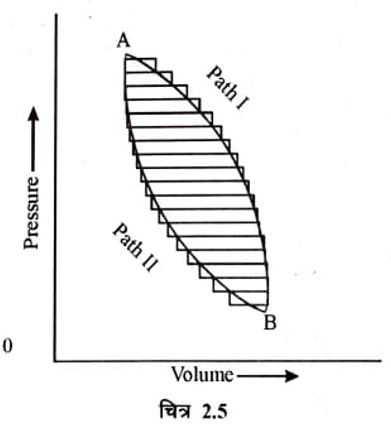
माना कि ABA एक उत्क्रमणीय चक्रीय प्रक्रम है। जिसमें अवस्था A से B में तथा वापस अवस्था A में उत्क्रमणीय रूप में परिवर्तन किया जाता है (चित्र 2.5 ) । चक्र ABA को छोटे-छोटे कान चक्रों का समूह माना जा सकता है अर्थात सम्पूर्ण चक्र समतापी एवं रूद्धोष्म प्रक्रमों की श्रेणी हैं। प्रत्येक कान चक्र के लिये ज्ञात है कि

अतः उत्क्रमणीय चक्र ABA के लिये उपरोक्त समीकरण को निम्न प्रकार से लिखा जा सकता है।

यदि परिवर्तन अनन्तसूक्ष्म हों तो उपरोक्त समीकरण निम्न रूप ले लेती है।

चूंकि सम्पूर्ण चक्र दो पदों AB तथा BA से बना है अतः समीकरण (30) को इस प्रकार भी लिखा जा सकता है।

समीकरण (41) से यह स्पष्ट है किव एक निश्चित राशि है जिसका मान परिवर्तन के पथ पर निर्भर नहीं करता, बल्कि अवस्था A तथा B पर निर्भर करता है। अतः यह राशि एक अवस्था फलन है, यह फलन एन्ट्रोपी कहलाता है। एन्ट्रोपी एक अवस्था फलन (State function) है।

यहाँ यह ध्यान रखना आवश्यक है कि ऊष्मा dq का अवशोषण उत्क्रमणीय ढंग से ही होना चाहिये

तंत्र द्वारा अवशोषित ऊष्मा धनात्मक होती है, अतः एन्ट्रोपी परिवर्तन भी धनात्मक होगा अतः तंत्र की एन्ट्रोपी ऊष्मा के अवशोषण के साथ बढ़ेगी तथा ऊष्मा विसर्जित होने पर घटेगी।

रूद्धोष्म उत्क्रमणीय परिवर्तनों में अवशोषित ऊष्मा शून्य होती है अतः एन्ट्रोपी परिवर्तन भी शून्य होगा। ऐसे प्रक्रम समएन्ट्रोपिक प्रक्रम (Isoentropic process) कहलाते हैं।

समतापी रूपान्तरण में एन्ट्रोपी परिवर्तन (Entropy Changes in Isothermal Transformation)

समतापी रूपान्तरणों जैसे, आदर्श गैस का समतापी प्रसार, प्रावस्था रूपान्तरण आदि में एन्ट्रोपी परिवर्तन की गणना की जा सकती है। इसके लिये हमको सम्बन्धित रूपान्तरण प्रक्रम में अवशोषित ऊष्मा की मात्रा ज्ञात करनी होती है। यहाँ यह ध्यान रखना चाहिये कि प्रक्रम उत्क्रमणीय ढंग से रूपान्तरित हो ।

आदर्श गैस के समतापी प्रसार में एन्ट्रोपी परिवर्तन (Entropy changes in Isothermal Expansion of an Ideal gas)-

मान लीजिये कि एक आदर्श गैस के n मोल का समतापी उत्क्रमणीय प्रसार किया जाता है। इस प्रसार में गैस की आन्तरिक ऊर्जा में कोई परिवर्तन नहीं होगा अतः E = 0 ऊष्मागतिकी के प्रथम नियम की समीकरण (E = q -w) में E का मान शून्य रखने पर

q=w

यहाँ q अवशोषित ऊष्मा तथा w प्रसार कार्य है।

या qrev =w ……….(44)

यदि गैस का प्रसार निश्चित ताप T पर आयतन V1 से V2 तक किया जाता है, तो समीकरण (1) द्वारा

एन्ट्रोपी में परिवर्तन समीकरण (35) द्वारा प्रदर्शित किया जाता है, अर्थात्

समीकरण (46) द्वारा एन्ट्रोपी परिवर्तन का मान ज्ञात किया जा सकता है।

भौतिक प्रावस्था में परिवर्तन पर एन्ट्रापी परिवर्तन (Entropy change in Physical State),

(1) ठोस प्रावस्था से द्रव प्रावस्था में रूपान्तरण में एन्ट्रोपी परिवर्तन (Entropy change in transformation of Solid in to Liquid phase):-

जब किसी ठोस को उसके गलनांक (Melting point ) पर ऊष्मा दी जाती है तो वह उसी ताप पर द्रव में परिवर्तित हो जाता है। इसके लिये आवश्यक ऊष्मा गलन की गुप्त ऊष्मा (Latent Heat of fusion) कहलाती है ।

माना कि 1 मोल ठोस को उत्क्रमणीय रूप से गलन बिन्दु Tf पर द्रव में परिवर्तित किया जाता है। इस परिवर्तन में माना कि स्थिर दाब पर Hfऊष्मा अवशोषित होती है। यह अवशोषित ऊष्मा गन की मोलर ऊष्मा (Molar heat of fusion) कहलाती है। समीकरण (35) अनुसार-

AS गलन प्रक्रम में एन्ट्रोपी परिवर्तन है। चूंकि AH धनात्मक है अतः AS का मान भी धनात्मक होगा ।

(2) द्रव-प्रावस्था से गैस प्रावस्था में रूपान्तरण में एन्ट्रोपी परिवर्तन (Entropy change in Transformation of Liquid in to Gas):– जब किसी द्रव को उसके क्वथनांक (Boiling point) पर ऊष्मा दी जाती है तो वह उसी ताप पर गैस में परिवर्तित हो जाता है। इस परिवर्तन के लिये आवश्यक ऊष्मा वाष्पन की गुप्त ऊष्मा (Latent heat of vaporisation) कहलाती है।

माना कि 1 मोल द्रव को उत्क्रमणीय रूप से क्वथनांक Tb पर गैस में परिवर्तित किया जाता है। इस परिवर्तन में माना कि स्थिर दाब पर Hv ऊष्मा अवशोषित होती है। यह अवशोषित ऊष्मा वाष्पन की मोलर ऊष्मा (Molar Heat of Vaporisation) कहलाती है। समीकरण (35) के अनुसार-

(3) एक क्रिस्टलीय अवस्था से दूसरी क्रिस्टलीय अवस्था में रूपान्तरण में एन्ट्रोपी परिवर्तन (Entropy change accompanying transformation of one crystalline form in to another)-

यदि एक मोल ठोस संक्रमण ताप पर एक क्रिस्टलीय अवस्था से दूसरी क्रिस्टलीय अवस्था में परिवर्तित हो तो अवशोषित या उत्सर्जित ऊष्मा (Heat of transition) या संक्रमण की मोलर ऊष्मा (Molar Heat of transition) कहलाती है।

यदि Ht संक्रमण ऊष्मा तथा T1 संक्रमण ताप हो तो मोलर एन्ट्रोपी परिवर्तन St को निम्न समीकरण द्वारा व्यक्त किया जा सकता है।

ताप व आयतन के फलन के रूप में एन्ट्रोपी (Entropy as a function of Temperature and Volume) जैसा कि पहले बताया जा चुका है. एन्ट्रोपी एक अवस्था फलन है। उसका मान किसी भी शुद्ध पदार्थ के लिये तीन ऊष्मागतिकी चरांको (P. V. T) में से दो चरांको द्वारा निर्धारित किया जा सकता है। इस खण्ड में एन्ट्रोपी को ताप व आयतन का फलन माना गया है।

चूंकि समीकरण (50) तथा ( 53 ) दोनों एन्ट्रोपी परिवर्तन T तथा V के रूप में प्रदर्शित करती है। अतः दोनों समीकरण समरूप है। इन दोनों समीकरणों की तुलना करने पर

चूंकि Cv/T हमेशा धनात्मक होता है अतः समीकरण (55) से यह निष्कर्ष निकाला जा सकता है कि निश्चित आयतन पर ताप बढ़ने से एन्ट्रोपी का मान बढ़ता है।

एक परिमित ताप परिवर्तन के मध्य स्थिर आयतन पर एन्ट्रोपी परिवर्तन

समीकरण (58) को स्थिर ताप पर V के संदर्भ में तथा समीकरण (59) को स्थिर आयतन पर T के संदर्भ में अवकलित करने पर

ताप व दाब के फलन के रूप में एन्ट्रोपी (Entropy as a Function of Temperature and Pressure)

इस खण्ड में माना कि एन्ट्रोपी ताप व दाब का फलन है। अतः

S = f(T, P)

पूर्ण अवकलन करने पर

ऊष्मागतिकी से व्युत्पन्न समीकरण H = E + PV का अवकलन करने पर

dH = dE + PdV + VdP ………………………(65)

समीकरण (51) द्वारा dE=TdS – PdV

या dE + PdV =Tds

अतः समीकरण (65) को निम्न प्रकार लिखा जा सकता है।

dH = T dS + VdP …………………….(66)

माना कि H ताप व दाब का फलन है

H = f (T,P)

इसका पूर्ण अवकलन करने पर

चूंकि Cp/ T हमेशा धनात्मकं होता है अतः समीकरण (70) से यह निष्कर्ष निकाला जा सकता है कि

निश्चिंत दाब पर ताप बढ़ाने से एन्ट्रोपी का मान बढ़ता है।

एक परिमित ताप परिवर्तन के मध्य स्थिर दाब पर एन्ट्रोपी परिवर्तन

समीकरण (69) तथा (71) को पुनः व्यवस्थित करने पर

समीकरण (73) को स्थिर ताप पर P के संदर्भ में तथा समीकरण (74) को स्थिर दाब पर T के संदर्भ में अवकलित करने पर

एन्ट्रोपी की दाब पर निर्भरता के लिये यह एक सरल समीकरण है।

समीकरण (63) तथा (78) पूर्णतया सामान्य (General) समीकरण है जो कि ठोस, द्रव व गैस के लिये समान रूप से उपयोगी है।

द्रवों के दाव परिवर्तन से एन्ट्रोपी परिवर्तन (Change in Entropy of a Liquid with Pressure) जैसा कि पूर्व में बताया गया है, समीकरण (78) प्रत्येक अवस्था के द्रव्य (ठोस, द्रव तथा गैस) के लिये उपयोग में ली जा सकती है।

यह समीकरण एन्ट्रोपी की दाब पर निर्भरता दर्शाती है। चूंकि ताप स्थिर है अर्थात् dT = 0

समीकरण मेंस्थिर दाब पर प्रसार गुणांक कहलाता है। परिभाषा के अनुसार प्रतिडिग्री ताप बढ़ाने पर आयतन में होने वाला परिवर्तन है। ठोस व द्रव के लिये इसका मान बहुत कम होता है। ठोसों में प्रसार गुणांक 10- 4K – 1 की कोटि का तथा द्रवों में 104 से 10-3K-1 की कोटि का होता है। अतः ठोस व द्रव के लियेको स्थिर माना जा सकता है।

माना कि द्रव पर दाब P1 से P2 बढ़ाया जाता है, तो एन्ट्रोपी परिवर्तन निम्न समीकरण द्वारा किया जा सकता है-

चूंकि द्रवों के लियेकी कोटि 10-3K- 1 होती है अतः समीकरण (70) से स्पष्ट है कि S जूल K-1 कमी के लिये दाब को लगभग 1000 वायुमण्डल बढ़ाना होगा। अर्थात् दाब के साथ द्रवों की एन्ट्रोपी में परिवर्तन बहुत कम होता है अतः इस परिवर्तन को उपेक्षणीय मान कर छोड़ दिया जाता है।