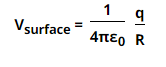आवेशित गोलीय कोश के कारण विद्युत विभव electric potential spherical shell

SbistudyJanuary 18, 2018inPhysics

विद्युत विभव का परिकलन (calculation of electric potential ) : अब हम विभिन्न प्रकार के पृष्ठो अर्थात आकृतियों के लिए विद्युत विभव के लिए परिकलन करेंगे।

सबसे पहले गोलीय कोश के लिए ज्ञात करेंगे , फिर आवेशित चालक गोले व अचालक गोले का अध्ययन करेंगे और इन सब पृष्ठो के कारण किसी बिंदु पर विभव का मान ज्ञात करेंगे और सूत्र स्थापित करेंगे।

आवेशित गोलीय कोश के कारण विद्युत विभव (electric potential due to charged spherical shell )

इस स्थिति में हम एक गोलीय कोश पर अध्ययन करेंगे जो आवेशित किया गया है।

माना एक R त्रिज्या का गोलीय कोश है , इस गोलीय कोश पर q आवेश विधमान है अर्थात यह गोलीय कोश q आवेश से आवेशित है।

अब हम r दूरी पर एक बिंदु P की परिकल्पना करते है और P बिन्दु पर विभव का मान ज्ञात कर सकते है , यहाँ ध्यान देने वाली यह बात है की P बिंदु की तीन स्थितियां संभव है।

1. जब P बिंदु गोलीय कोश के बाहर स्थित हो अर्थात r > R

2. जब P बिंदु गोलीय कोश के पृष्ठ पर स्थित हो अर्थात r = R

3. जब P बिंदु गोलीय कोश के अंदर स्थित हो अर्थात r < R

अब हम तीनो स्थितियों को अध्ययन करेंगे

1. जब P बिंदु गोलीय कोश के बाहर स्थित हो अर्थात r > R

जब बिंदु गोलीय कोश के बाहर (r > R ) स्थित है अर्थात हमें विभव का मान कोश के बाहर स्थित किसी बिन्दु P पर ज्ञात करना है।

हम विद्युत विभव की परिभाषा में पढ़ चुके है
V = – _∞∫^rE.dr
हम यह भी पढ़ चुके है की गोले के बाहर स्थित बिंदु P पर विद्युत क्षेत्र

E का मान सूत्र में रखने पर

सूत्र से यह बात हम स्पष्ट रूप से देख सकते है की गोलीय कोश के बाहर स्थित बिंदु पर विभव का मान दुरी के व्युत्क्रमानुपाती होता है।

2. जब P बिंदु गोलीय कोश के पृष्ठ पर स्थित हो अर्थात r = R

अब हम बात करते है जब P बिंदु गोलीय कोश के पृष्ठ पर स्थित है , इस स्थिति में r = R होता है।

हम जानते है की

V = – _∞∫^RE.dr

हमने ज्ञात किया है

इस स्थिति में r = R है अतः r के स्थान पर R रखने पर हमें पृष्ठ पर विद्युत विभव का मान प्राप्त होता है

3. जब P बिंदु गोलीय कोश के अंदर स्थित हो अर्थात r < R

जब P बिंदु गोलीय कोश के अंदर स्थित हो अर्थात इस दशा में r < R होगा , इस स्थिति में विभव का मान ज्ञात करते है

हम जानते है की

V = – _∞∫^rE.dr

यहाँ इसे दो भागों में हल करते है

a . अनंत दूरी से पृष्ठ (R) तक

b . R (पृष्ठ) से P बिंदु तक अर्थात r दुरी तक

V = – _∞∫^RE.dr + (– _R∫^rE.dr)

चूँकि कोश के भीतर विद्युत क्षेत्र की तीव्रता (E) का मान शून्य हो जाता है अतः दूसरा भाग शून्य हो जाता है।

अतः P बिंदु पर विभव का मान सिर्फ पहले भाग के कारण ही होगा।

अतः कोश के अंदर विद्युत विभव

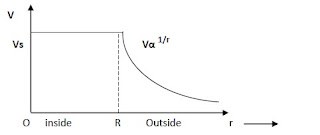
सूत्रों का अध्ययन करने से हम पाते है की पृष्ठ के भीतर स्थित किसी बिंदु पर विद्युत विभव का मान पृष्ठ पर विभव के मान के बराबर होता है तथा पृष्ठ के बाहर यह r (दूरी) के व्युत्क्रमानुपाती होता है अतः पृष्ठ व अंदर विभव का मान अधिकतम होता है।

आवेशित गोलीय कोश द्वारा उत्पन्न विभव व केंद्र से बिंदु P की दुरी के मध्य ग्राफ (graph) खींचने पर वह निम्नानुसार प्राप्त होता है।