विद्युत फ्लक्स (Φ) (electric flux) , आवेश वितरण , रेखीय , पृष्ठीय , आयतन आवेश वितरण , घनत्व

SbistudyAugust 26, 2019inPhysics

गाउस का नियम एवं उसके अनुप्रयोग :

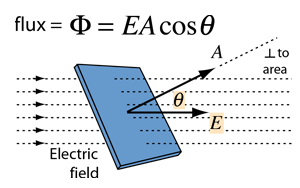
विद्युत फ्लक्स (Φ) (electric flux) : विद्युत क्षेत्र में स्थित किसी पृष्ठ के तल के लम्बवत गुजरने वाली विद्युत बल रेखाओ की संख्या को ही विद्युत फलस्क कहते है।

अथवा

विद्युत क्षेत्र की तीव्रता तथा पृष्ठ के क्षेत्रफल के क्षेत्रफल सदिश का अदिश गुणनफल पृष्ठ से सम्बद्ध विद्युत फलस्क के बराबर होता है।

अर्थात

विद्युत फलस्क dΦ= E.dS (वेक्टर फॉर्म में)

dΦ= E.dS.cosθ

सम्पूर्ण खुले पृष्ठ से सम्बन्ध कुल फलस्क (Φ) = ∫E.dS

सम्पूर्ण बन्द पृष्ठ से सम्बन्ध कुल फलस्क (Φ) = ∫E.dS

विद्युत फलस्क एक अदिश राशि है।

विधुत फलस्क का मात्रक N-m²/C या J-m/C है।

विद्युत फलस्क की विमा [M¹L³T^-3A^-1] होती है।

किसी पृष्ठ में प्रवेश करने वाली विद्युत बल रेखाओ के कारण फलस्क सदैव ऋणात्मक होता है तथा बाहर निकलने वाली बल रेखाओ के कारण फलस्क सदैव धनात्मक होता है।

विद्युत क्षेत्र में स्थित किसी पृष्ठ में जितनी विद्युत बल रेखायें प्रवेश करती है यदि उतनी ही बल रेखाएं बाहर निकलती हो तो पृष्ठ से सम्बन्ध कुल फलस्क शून्य होता है।

आवेश वितरण : आवेश वितरण मुख्यतः तीन प्रकार के होते है –

1. रेखीय आवेश वितरण : यदि किसी आवेश का एक रेखा के रूप में समान रूप से वितरण हो तो इसे रेखीय आवेश वितरण कहते है।

रेखीय आवेश घनत्व (λ) : एकांक लम्बाई पर उपस्थित आवेश की मात्रा को ही , रेखीय आवेश घनत्व कहते है।

अर्थात रेखीय आवेश घनत्व

[λ = q/l]

रेखीय आवेश घनत्व का मात्रक = कुलाम/मीटर या एम्पियर x सेकंड/मीटर

विमा :

2. पृष्ठीय आवेश वितरण : जब किसी आवेश का एक पृष्ठ के रूप में समान रूप से वितरण हो तो इसे पृष्ठीय आवेश वितरण कहते है।

पृष्ठीय आवेश घनत्व (σ) : एकांक क्षेत्रफल पर उपस्थित आवेश की मात्रा को ही पृष्ठीय आवेश घनत्व कहते है।

पृष्ठीय आवेश घनत्व

[σ = q/A]

पृष्ठीय आवेश घनत्व का मात्रक = कुलाम/मीटर² या ” एम्पियर x सेकंड/मीटर^{2 “} है।

विमा : [M⁰ L^-2 T¹ A¹]

3. आयतन आवेश वितरण : जब किसी आवेश एक आयतन के रूप में समान रूप से वितरण हो तो इसे आयतन आवेश वितरण कहते है।

आयतन आवेश घनत्व (p) : एकांक आयतन में उपस्थित आवेश की मात्रा को ही आयतन आवेश घनत्व कहते है।

अर्थात आयतन आवेश घनत्व [p = q/V]

आयतन आवेश घनत्व का मात्रक = कुलाम/आयतन या ” एम्पियर x सेकंड /मीटर³ ” है।

विमा : [M⁰ L^-3 T¹ A¹] है।

गाउस का नियम

निर्वात या वायु में स्थित किसी काल्पनिक बन्द पृष्ठ से सम्बन्ध विद्युत फलस्क का मान उस बंद पृष्ठ से परिबद्ध कुल आवेश तथा 1/E₀ के गुणनफल के बराबर होता है।

अर्थात

Φ = Σq/E₀

किसी बंद पृष्ठ से सम्बद्ध कुल फलस्क = ∫ E.dS = Σq/E₀

गाउस के नियम से सम्बन्धित महत्वपूर्ण बिन्दु :

गाउस का नियम बंद पृष्ठ के आकार व आकृति पर निर्भर नहीं करता है।
गाउस का नियम बन्द पृष्ठ में आवेश के वितरण पर भी निर्भर नहीं करता है।
गाउस का नियम बंद पृष्ठ से बाहर स्थित आवेश की मात्रा पर निर्भर नहीं करता है।
गाउस का नियम बंद पृष्ठ में उपस्थित आवेश की मात्रा पर निर्भर करता है।
गाउस का नियम बंद पृष्ठ में उपस्थित माध्यम पर निर्भर करता है।
जब किसी बंद पृष्ठ में प्रवेश करने वाली बल रेखाओ की संख्या बाहर निकलने वाली बल रेखाओ की संख्या से कम हो तो पृष्ठ से सम्बद्ध कुल फलस्क धनात्मक होगा अर्थात बंद पृष्ठ में धनावेश उपस्थित होगा।
जब किसी बंद पृष्ठ में प्रवेश करने वाली बल रेखाओ की संख्या बाहर निकलने वाली बल रेखाओ की संख्या से अधिक हो तो बंद पृष्ठ से समद्ध कुल फलस्क ऋणात्मक होगा अर्थात बंद पृष्ठ में ऋणावेश उपस्थित होगा।
जब किसी बंद पृष्ठ में प्रवेश करने वाली बल रेखाओ की संख्या , बाहर निकलने वाली बल रेखाओ की संख्या के समान हो तो बंद पृष्ठ से सम्बद्ध कुल फलस्क शून्य होगा। अर्थात या तो बंद पृष्ठ में कोई आवेश उपस्थित नहीं होगा या फिर द्विध्रुव के रूप में आवेश उपस्थित होगा।

कूलाम नियम द्वारा गाउस के नियम की उत्पत्ति :

माना कोई बिन्दु O जिस पर ‘q’ आवेश स्थित है इस आवेश को स्वेच्छिक बंद पृष्ठ में रखते है। इस q आवेश से r दूरी पर स्थित पृष्ठ पर विद्युत क्षेत्र की तीव्रता –