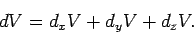relation between electric field and electric potential in hindi विद्युत क्षेत्र एवं विद्युत विभव में सम्बन्ध : विद्युत क्षेत्र से विद्युत विभव के सूत्र स्थापन में हमने एक सम्बन्ध स्थापित किया था और इस संबंध के अनुसार दो बिंदुओं के मध्य विभवांतर तथा विद्युत क्षेत्र की तीव्रता निम्न प्रकार से सम्बन्धित है।
VB – VA = –A∫B E.dl
यहाँ VB B बिंदु पर विभव
VA A बिंदु पर विभव
VB – VA = दोनों बिंदुओं के मध्य विभव में अंतर (विभवान्तर )
E = विद्युत क्षेत्र की तीव्रता
dl = अल्पांश dl विस्थापन
यहाँ हम विद्युत क्षेत्र तथा विद्युत विभव में सम्बन्ध स्थापित करेंगे।
विद्युत क्षेत्र की तीव्रता (E) में अल्प विस्थापन dl के लिए निम्न प्रकार लिखा जा सकता है।
VB – VA = –A∫B E.dl
अवकलन लेने पर
(VB – VA) = – E.dl
बिंदु VA को अनंत पर मानने पर VA = 0 व्यापक रूप
d(V) = -Edl
dV = -Edl COSθ
यहाँ θ , E व dl के मध्य कोण
यहाँ -dV/dl दूरी के साथ विभव में कमी को दर्शाता है अर्थात यह दर्शाता है की दूरी बढ़ने पर विभव कम होता जाता है।
जब E व dl के मध्य कोण का मान शून्य होगा तब विभव में दुरी के साथ कमी अधिकतम होती है।
सामान्यतया dV/dl एक अदिश राशि होती है लेकिन θ = 0 पर dV/dl विभव में अधिकतम कमी को सदिश माना जा सकता है इसकी दिशा E की दिशा में होती है , इसे विभव प्रवणता कहते है , इसे grad V से प्रदर्शित किया जाता है।
चूँकि
-dV/dl = E
अतः
E = -Grad V
समविभव पृष्ठ के लिए विभव प्रवणता की दिशा पृष्ठ के लंबवत होती है।
माना चित्रानुसार दो समविभव पृष्ठ दिए गए है एक पृष्ठ के विभव का मान V तथा दूसरे पर विभव V-dV है।
चूँकि B तथा C बिंदु पर विभव का मान समान है अतः A बिन्दु से B व C के लिए विभव में कमी या हानि का मान समान dV होगा।
लेकिन AB व AC की दूरी भिन्न भिन्न है अतः विभव में दूरी के साथ परिवर्तन की दर भी अलग अलग dV/AB व dV/AC होगी।
क्योंकि दूरी AC का मान AB से अधिक है अर्थात AB < AC है अतः dV/AB > dV/AC
यहाँ विभव में हानि की दर पृष्ठ के अभिलम्ब दिशा में अधिकतम होगा।
यहां हम l को एक अक्ष मानकर समीकरण ज्ञात कर रहे है।
El = E COSθ , dl की दिशा में E
यदि अक्ष x , y , z अक्षो में है तो
समविभव पृष्ठ के लिए विभव प्रवणता की दिशा पृष्ठ के लंबवत होती है।
माना चित्रानुसार दो समविभव पृष्ठ दिए गए है एक पृष्ठ के विभव का मान V तथा दूसरे पर विभव V-dV है।
चूँकि B तथा C बिंदु पर विभव का मान समान है अतः A बिन्दु से B व C के लिए विभव में कमी या हानि का मान समान dV होगा।
लेकिन AB व AC की दूरी भिन्न भिन्न है अतः विभव में दूरी के साथ परिवर्तन की दर भी अलग अलग dV/AB व dV/AC होगी।
क्योंकि दूरी AC का मान AB से अधिक है अर्थात AB < AC है अतः dV/AB > dV/AC
यहाँ विभव में हानि की दर पृष्ठ के अभिलम्ब दिशा में अधिकतम होगा।
यहां हम l को एक अक्ष मानकर समीकरण ज्ञात कर रहे है।
El = E COSθ , dl की दिशा में E
यदि अक्ष x , y , z अक्षो में है तो
चूँकि
अतः
अतः
E = ∇ V
यहाँ इसे ∇ को डेल संकारक (del operator) कहते है।
यदि यहां विभव को गोलीय पृष्ठ के लिए अर्थात त्रिज्या r के रूप में लिखने पर
Er = -dV/dr