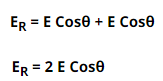विद्युत द्विध्रुव के कारण उसकी निरक्ष रेखा या विषुवतीय रेखा पर स्थित बिंदु पर विद्युत क्षेत्र electric field

हमने विद्युत द्विध्रुव के कारण उसकी अक्ष पर विद्युत क्षेत्र की तीव्रता ज्ञात की थी जिसमे हमने यह निष्कर्ष निकाला था की अक्ष पर विद्युत क्षेत्र की तीव्रता एकल आवेश की भाँती 1/r² के समानुपाती न होकर 1/r³  के समानुपाती होती है अर्थात एकल आवेश के कारण विद्युत क्षेत्र की तुलना में यह दूरी के साथ तेजी से घटती है।

अब हम बात करते है विद्युत द्विध्रुव के कारण इसकी निरक्ष रेखा पर विद्युत क्षेत्र की तीव्रता कितनी होगी ?

माना एक द्विध्रुव आघूर्ण AB है , A बिंदु पर -q आवेश रखा है तथा B बिन्दु पर +q आवेश रखा है।  दोनों आवेशों के मध्य की दुरी 2a है।  द्विध्रुव आघूर्ण के केंद्र O से r दुरी पर निरक्ष पर एक बिंदु P स्थित है तथा हमें द्विध्रुव आघूर्ण के कारण इस P बिंदु पर विद्युत क्षेत्र की तीव्रता ज्ञात करनी है।

बिंदु P से दोनों आवेशों की दुरी समान होगी और यह दूसरी (√r² + a²) होगी। 
+q आवेश के कारण बिन्दु P पर विद्युत क्षेत्र की तीव्रता 

इसकी दिशा BP के अनुदिश होगी। 
-q आवेश के कारण बिन्दु P पर विद्युत क्षेत्र की तीव्रता 

इसकी दिशा PA के अनुदिश होगी।
दोनों सूत्रों से यह स्पष्ट है की दोनों आवेशों के कारण P बिंदु पर विद्युत क्षेत्र की तीव्रता का मान बराबर होता है किन्तु दोनों की दिशा भिन्न भिन्न है। 
E_+q = E_-q = E
चित्र से स्पष्ट है की E_+q तथा  E_-q के दो प्रकार के घटक बनते है , एक घटक बनता है अक्षीय रेखा के लंबवत तथा दूसरा घटक अक्षीय रेखा के अनुदिश। 
अक्षीय रेखा के लंबवत बने घटक E_+q Sinθ व  E_-q Sinθ , परिमाण में बराबर है किन्तु दिशा में विपरीत है अतः ये एक दूसरे को निरस्त कर देते है।
अक्षीय रेखा के अनुदिश घटक E_+q Cosθ व  E_-q Cosθ दोनों एक ही दिशा में अतः ये दोनों जुड़ जाते है।
अतः परिणामी विद्युत क्षेत्र की तीव्रता

Cosθ का मान रखने पर 

मान रखने पर परिणामी विद्युत क्षेत्र की तीव्रता 

चूँकि हम जानते है की 2qa = p (विद्युत द्विध्रुव आघूर्ण) अतः इसका मान रखने पर 

माना a का मान r की तुलना में अत्यन्त कम है अतः r² की तुलना में a² का मान नगण्य मानकर छोड़ने पर  

अक्ष पर स्थित बिंदु पर विद्युत क्षेत्र की तीव्रता उतनी ही दूरी पर निरक्षीय बिंदु पर विद्युत क्षेत्र की तीव्रता की दो दोगुनी होती है।
(E_axial) = 2(E_equatorial)
निरक्ष पर स्थित बिंदु पर विद्युत क्षेत्र की दिशा विद्युत आघूर्ण के विपरीत दिशा में होती है। 

निरक्षीय स्थिति में विद्युत द्विध्रुव के कारण उत्पन्न वैद्युत क्षेत्र की तीव्रता : विद्युत द्विध्रुव की निरक्षीय स्थिति में r दूरी पर स्थित बिंदु P पर विद्युत क्षेत्र की तीव्रता ज्ञात करनी है। बिंदु P से दोनों आवेशो की दूरियाँ समान √(r² + l²) होंगी अत: P पर +q आवेश के कारण उत्पन्न विद्युत क्षेत्र की तीव्रता का परिमाण निम्न सूत्र द्वारा दिया जाता है –

E₁ = q/4πε₀(r² + l²)

तथा -q आवेश के कारण P पर उत्पन्न विद्युत क्षेत्र की तीव्रता का परिमाण –

E₂ = q/4πε₀(r² + l²)

अत: इस तरह |E₁| = |E₂|

बिंदु P पर परिणामी विद्युत क्षेत्र की तीव्रता –

E = E₁ +  E₂

समान्तर चतुर्भुज के नियम से परिणामी विद्युत क्षेत्र की तीव्रता का परिमाण –

E = √(E₁² + E₂² + 2E₁E₂cos2θ)

चूँकि  |E₁| = |E₂|

E = √(E₁² + E₁² + 2E₁E₁cos2θ)

E = √(2E₁² + 2E₁²cos2θ)

E = √(2E₁²(1 + cos2θ)

E = E₁√2(1 + 2cos²θ – 1)

E = √2×2 cos²θ

E = 2E₁cosθ

चूँकि चित्र से cosθ = l/√(r² + l²)

E₁ व cosθ का मान रखने पर –

E = 2 x q/4πε₀(r² + l²) x l/√(r² + l²)

हल करने पर

E = q.2l/ 4πε₀(r² + l²)^3/2

या

चूँकि q.2l = p

E = p/ 4πε₀(r² + l²)^3/2

चित्र में E की दिशा द्विध्रुव की अक्ष के समान्तर होगी। चूँकि द्विध्रुव आघूर्ण p की दिशा ऋण आवेश से धन आवेश की ओर होती है अत: विद्युत क्षेत्र E एवं विद्युत द्विध्रुव p की दिशाएँ परस्पर विपरीत होंगी।

दीर्घ परास की दूरियों के लिए  r>> l

अत:  r² >> l²

अत: l² को r² की तुलना में नगण्य मानकर छोड़ने पर –

E = p/ 4πε₀r³

^{याद रखे कि}  विद्युत क्षेत्र E एवं विद्युत द्विध्रुव p की दिशा विपरीत होगी।