1. दे ब्रोग्ली सिद्धांत : जिस प्रकार से प्रकाश की द्वेत प्रकृति होती है , उसी प्रकार से
द्रव्य के कण (
इलेक्ट्रॉन ,
प्रोटोन और
न्यूट्रॉन) की भी द्वेत प्रकृति होती है , यह तथ्य द ब्रोग्ली द्वारा दिया गया था इसलिए इसे दे ब्रोग्ली का सिद्धान्त कहते है।
इसके अनुसार द्रव्य के कण (इलेक्ट्रॉन , प्रोटोन और न्यूट्रॉन) तरंग के रूप में
गति करते है और इन तरंगो की
तरंग दैर्ध्य संवेग के व्युत्क्रमानुपाती होता है।
दे ब्रोग्ली ने आइन्स्टीन समीकरण और प्लांक समीकरण की सहायता से तरंग दैर्ध्य (λ) और संवेग (p ) के मध्य निम्न सम्बन्ध स्थापित किया।
E = mc2 (आइन्स्टीन समीकरण)
E = hv (प्लांक समीकरण)
दोनों समीकरण की तुलना करने पर –
hv = mc2
चूँकि v = c/ λ
इसलिए
hc/ λ = mc2
h/ λ = mc
1/ λ = mc/h
Λ = h/mc
यहाँ ;
c प्रकाश का वेग , इलेक्ट्रॉन के लिए c के स्थान पर v लिया जाता है
अर्थात λ = h/mv
संवेग (p) = द्रव्यमान (m) x वेग (v)
Λ = h/p
Λ ∝ 1/p
जहाँ h = प्लांक नियतांक (6.626070150(81)×10−34 J.s)
m = इलेक्ट्रॉन का द्रव्यमान
Λ = तरंग दैधर्य
c =
प्रकाश का वेग
दे ब्रोग्ली सिद्धांत की सार्थकता
यह सिद्धान्त द्रव्य के छोटे कण (इलेक्ट्रॉन , प्रोटोन और न्यूट्रॉन) के लिए ही मान्य है परन्तु द्रव्य के भारी कणों के लिए यह सिद्धांत मान्य नहीं है।
क्रिकेट की बॉल की भी द्वेत प्रकृति होती है अर्थात कणीय और तरंगीय प्रकृति होती है लेकिन इसका वजन अधिक होने के कारण तरंग दैधर्य का मान बहुत कम होता है , तरंग दैधर्य के इस बहुत कम मान को प्रयोगों द्वारा ज्ञात नहीं किया जा सकता है अत: दे ब्रोगली सिद्धांत केवल सूक्ष्म कणों के लिए ही लागू होता है।
द्रव्य की कणीय और तरंगीय प्रकृति के बाद हाइजेन वर्ग ने बताया कि किसी क्षण विशेष पर इलेक्ट्रॉन की स्थिति तथा संवेग दोनों को एक साथ यथार्थता (सत्यता) के साथ ज्ञात नहीं किया जा सकता है।
यदि किसी क्षण विशेष पर इलेक्ट्रॉन की स्थिति ज्ञात करने में न्यूनतम त्रुटी △μ और संवेग ज्ञात करने में न्यूनतम त्रुटी △p है तो हाइजेन वर्ग के अनुसार इन दोनों का गुणनफल h/4λ से अधिक या इसके बराबर होता है।
△μ.△p ≥ h/4λ
चूँकि △p = m △v
इसलिए
△μ.m △v = h/4λ
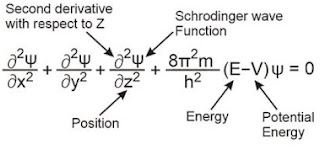
देब्रोग्ली और हाइजेन वर्ग के अनिश्चितता सिद्धांत के आधार पर श्रोडिंगर ने परमाणु का एक नया प्रतिरूप विकसित किया जिसे क्वांटम यांत्रिकी या तरंग यान्त्रिकी प्रतिरूप कहते है , इस प्रतिरूप में इलेक्ट्रॉन के व्यवहार को एक समीकरण के रूप में प्रस्तुत किया गया जिसे श्रोडिंगर का “तरंग समीकरण” कहते है।
श्रोडिंगर ने उपरोक्त समीकरण को हल करके तरंग फलन (Ψ) का मान ज्ञात किया। तरंग फलन तरंग के आयाम को व्यक्त करता है।
जबकि तरंगफलन का वर्ग (Ψ2) अर्थात नाभिक के चारों ओर इलेक्ट्रॉन पाए जाने की सम्भावना को व्यक्त करता है। Ψ का जितना अधिक होता है , नाभिक के चारों ओर इलेक्ट्रॉन के पाए जाने की सम्भावना उतनी ही अधिक होती है।
कक्षक / इलेक्ट्रॉन अभ्र : नाभिक के चारों ओर का वह क्षेत्र जहाँ पर इलेक्ट्रॉन के पाए जाने की सम्भावना सबसे अधिक होती है उसे कक्षक कहते है।
समभ्रंश कक्षक : समान ऊर्जा के कक्षकों को समभ्रंश कक्षक कहते है।
क्रोड़ इलेक्ट्रॉन : पूर्ण रूप से भरे कोशों के इलेक्ट्रॉनो को क्रोड़ इलेक्ट्रॉन कहते है।
नोडीय पृष्ठ : वह क्षेत्र जहाँ पर इलेक्ट्रॉन के पाए जाने की सम्भावना शून्य होती है उसे नोडीय पृष्ठ कहते है , नोडीय पृष्ठ हमेशा s कक्षकों के लिए ज्ञात किये जाते है।
1s कक्षक के लिए नोडीय पृष्ठ = 0
2s कक्षक के लिए नोडीय पृष्ठ = 1
3s कक्षक के लिए नोडीय पृष्ठ = 2
4s कक्षक के लिए नोडीय पृष्ठ = 3
Ns कक्षक के लिए नोडीय पृष्ठ = N – 1
नोडीय तल :वह तल जहाँ पर इलेक्ट्रॉन के पाए जाने की सम्भावना शून्य होती है उसे नोडीय तल कहते है , नोडीय तल p और d कक्षकों के लिए ही ज्ञात किया जाता है।
नोडीय तल =(n – l + 1)
tags : de broglie equation in hindi ?