बेलनाकार अनुनादी कोटर क्या है CYLINDRICAL RESONANT CAVITY in hindi physics

CYLINDRICAL RESONANT CAVITY in hindi physics बेलनाकार अनुनादी कोटर क्या है ?

वृत्ताकार बेलनीय निर्देशांकों में हेल्महोल्टज समीकरण (HELMHOLTZ EQUATION IN CIRCULAR CYLINDRICAL COORDINATES) 

निम्न प्रकार के अवकल समीकरण को हेल्महोल्टज समीकरण कहते हैं।

वृत्ताकार बेलनी निर्देशांकों (p, 0,z) में इस समीकरण को लिखने पर,

चरों की पृथक्कीरण विधि का उपयोग करते हुए इस समीकरण के हल को पृथक-पृथक एकल चर का फलन के गुणनफल के रूप में व्यक्त किया जा सकता है –

इसको समीकरण (1) में रखकर  से भाग देते हैं

इस समीकरण का तीसरा पद केवल 2 निर्देशांक पर निर्भर करता है इसलिए यह पद किसी नियतांक के बराबर होना चाहिये। माना यह नियतांक – B2 है।

यह साधारण अवकल समीकरण है जिसका हल है।

समीकरण (3) के तीसरे पद को – B2 से प्रतिस्थापन कर p2 से गुणा करने पर,

इस समीकरण का दूसरा पद भी केवल निर्देशांक  पर निर्भर करता है इसलिये यह पद किसी नियतांक के बराबर होना चाहिये । माना यह नियतांक – n 2 है। ‘

यह भी पेहले जैसा ही साधारण अवकल समीकरण है जिसका हल होगा

समीकरण (5) के दूसरे पद को – n 2 से प्रतिस्थापन करने पर,

इसको सरल करने के लिये, माना

यह समीकरण n कोटि का बेसल समीकरण है जिसका हल है-

जहाँ Jn(p) बेसल फलन तथा Na(p) न्यूनमान फलन है।

अतः हेल्महोल्ट्ज समीकरण का हल होगा-

 p = 0 पर परिमित रखने के लिये गुणांक F को शून्य के बराबर रखना पड़ेगा। अतः

यदि समस्या में दिगंशू सममिति है तो किसी विशिष्ट मान के लिये अक्ष p = 0 को इस प्रकार घूर्णित किया जा सकता है कि गुणांक C या D में से कोई एक शून्य बराबर हो जाये। अतः यदि C = 0 तो

जहाँ A1 = ADE_तथा_ B = BDE नये नियतांक हैं।

 बेलनाकार अनुनादी कोटर (CYLINDRICAL RESONANT CAVITY)

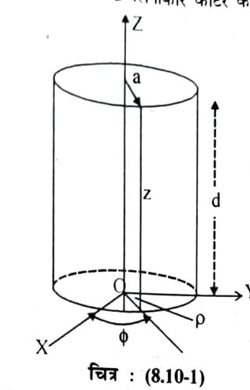
बेलनाकार कांटर चालक पृष्ठों से बना एक बेलनाकार आकृति की खोखली ट्यूब होती है जैसा कि चित्र (8.10-1-) दिखाया गया है। इसमें दो वृतीय पृष्ठ z = 0 व z = d होते है तथा एक बेलनाकार पृष्ठ p= a होता है जहाँ a व d बेलनाकार कोटर की क्रमशः त्रिज्या एवं लम्बाई है।

जब इसे अनुप्रस्थ विद्युत चुम्बकीय तरंगों (transverse electromagnetic waves) से उत्तेजित किया जाता है तो किसी विशिष्ट आवृति (frequency) पर अनुनाद करने लग जाता है। कोटर के अंदर विद्युत चुम्बकीय तरंगें मैक्सवेल समीकरणों (Maxwell equations) को संतुष्ट करती है। ये तरंगे परिसीमा प्रतिबंध को भी संतुष्ट करती है अर्थात कोटर के चालक पृष्ठ पर विद्युत क्षेत्र का स्पर्शीय घटक का मान शून्य होता है। अतः z = 0 वz =d पर Ep = Ep =0 तथा p = a पर Ep = Ez = 0 होता है।

मुक्ताकाश में विद्युत चुम्बकीय तरंगों के लिये मैक्सवेल समीकरणों से,

जहाँ विद्युतचुम्बकीय तरंगों की समय निर्भरता exp (jot) मानी गई है जहाँ ( विद्युतचुम्बकीय तरंग की आवृति है । समीकरण (IC) का कर्ल लेने पर,

इसमें समीकरण (la) व (ld) का उपयोग करने पर निम्न विद्युत क्षेत्र का तरंग समीकरण प्र होता है।

इसी प्रकार चुम्बकीय क्षेत्र के लिये भी तरंग समीकरण प्राप्त कर सकते है।

विद्युत व चुम्बकीय क्षेत्र के प्रत्येक घटक का तरंग समीकरण भी समीकरण (2) या (3) के समान होता है तथा ये समीकरण हेल्महोल्ट्ज समीकरण के समान है। अतः इन घटकों के मान हेल्महोल्ट्ज समीकरण के हल के समान होगा।

माना विद्युतचुम्बकीय तरंग के विद्युत क्षेत्र का z घटक z- अक्ष के अनुदिश संचरण कर रहा है तो खण्ड (8.7) के समीकरण ( 10 ) से,

अब मैक्सवेल समीकरण ( 1c ) को बेलनी निर्देशांकों में लिखने पर,

जिसका त्रिज्या घटक होगा,

इसी प्रकार समीकरण (ld) से,

बेलनाकार कोटर में, विद्युतचुम्बकीय तरंगें अनुप्रस्थ विद्युत [transverse electric (TE)] या अनुप्रस्थ चुम्बकीय [transverse magnetic (TM)] विधा ( mode) में उत्पन्न की जा सकती है। TE विधा में विद्युत क्षेत्र का अनुदैर्ध्य घटक अर्थात Ez घटक शून्य होता है तथा TM विधा में चुम्बकीय क्षेत्र का अनुदैर्ध्य घटक अर्थात Bz घटक शून्य होता है। बेलनाकार कोटर में विभिन्न विधाओं की एक निश्चित आवृति से अधिक आवृति की तरंगें ही संचरित हो सकती है अर्थात प्रत्येक विधा के लिये एक निश्चित आवृति होती है जिसे उस विधा की अंतक आवृति (cut-off frequency) कहते हैं।

वह विधा जिसके लिये अंतक आवृति न्यूनतम होती है उसे प्रमुख विधा (dominant mode) कहते हैं। अब हम पहले बेलनाकार कोटर में TM तरंग के प्रमुख विधा TM010 के संचरण पर विचार करते है। इस विधा में Bz = 0 होता है। समीकरण (6) में Bz = 0 रखने पर

इसमें समीकरण (5) रखने पर,

समीकरण (4) से,

इस अवकल का उपयोग समीकरण (7) में करने पर,

समीकरण (4) इसमें रखने पर,

अब समीकरण (10) में अंतिम परिसीमा प्रतिबंध p = a पर E2 = 0 रखने पर,

चूंकि बेसल फलन एक आवृतिक फलन होता है इसलिये Jn(x) = 0 के लिये अनंत हल होते है। माना समीकरण (11) का हल Ynp है, जहाँ n बेसल का फलन की कोटि है तथा p हल का क्रम है।

n = 0, p = 1 तथा q = 0 रखकर TM010 विधा की मूल अनुनादी आवृति ज्ञात की जा सकती  प्रमुख विधा के लिये Ynp 2.405 प्राप्त होता है। ये मान समीकरण ( 12 ) में रखने पर, है।

अतः प्रमुख TM010 विधा की मूल अनुनादी आवृति बेलनाकार कोटर की लम्बाई d पर निर्भर नहीं करती है।

TE विधा जिसमें Ez = 0 होता है, की मूल अनुनादी आवृति ज्ञात करने के लिये उपरोक्त TM विधा की भांति विधि अपना सकते हैं।

TE विधा के लिये अनुनादी आवृति का सम्बन्ध होगा

बेसल फलन के प्रथम अवकलज Jn (x) = 0 का हल

TM010 विधा d < 2a के लिये प्रमुख विधा रहती है परंतु d> 2a होने पर, TE। प्रमुख विधा हो जाती है। इस विधा के लिये ’11 = 1.841.

TE111 विधा की मूल अनुनादी आवृति