curvilinear coordinate system in hindi System वक्र रेखी निर्देश तंत्र क्या है

वक्र रेखी निर्देश तंत्र क्या है curvilinear coordinate system in hindi System ?

अध्याय 1 वक्र रेखी निर्देश तंत्र (Curvilinear Coordinate System)

 वक्र रेखी निर्देश तंत्र ( CURVILINEAR COORDINATE SYSTEM)

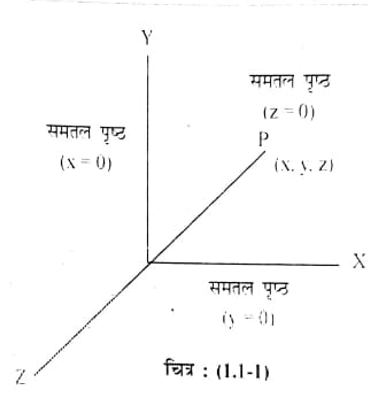
आकाश में किसी बिंन्दु की स्थिति को व्यक्त करने के लिए निर्देश तंत्र की आवश्यकता होती है। यह निर्देश तंत्र ऐसा होना चाहिए कि भिन्न-भिन्न कणों की स्थितियों में परस्पर सम्बन्ध स्थापित हो सकं। सबसे सरल तंत्र कार्तीय निर्देश तंत्र ( Cartesian coordinate system) होता है। यह निर्देश तंत्र तीन लम्बवत् समतल पृष्ठों (plane surfces) = 0. y = 0 तथा z = 0) से बना निकाल होता है। किन्हीं दो पृष्ठों के प्रतिच्छेदन से बनने वाली सरल रेखा निर्देशांक अक्ष (coordinate aves) कहलाती है। समतल x = 0 y = 0 पृष्ठों के प्रतिच्छेदन से z-अक्ष, y = 0 व z = 0 समतल पृष्ठों के प्रतिच्छंदन से -अक्ष तथा z = 0 त्र x = 0 पृष्ठों के प्रतिच्छेदन से y-अक्ष बनते हैं। तीनों अक्षों NNZ के प्रतिच्छेद बिन्दु को मूल बिन्दु (origin) या प्रेक्षक की स्थिति कहते हैं। चित्र (1.1-1 ) में तीनों अक्ष N Vz व मूल बिन्दु को 0 से दर्शाया गया है।

इस निर्देश तंत्र में किसी बिन्दु की स्थिति तीन राशियों 2 ) के एक समुच्चय से ज्ञात की जाती है जहाँ यह स्थिति (x, y, z) समतल पृष्ठों x k ( नियतांक ), y = kg ( नियतांक ) तथा z. kg ( नियतांक) का प्रतिच्छंद बिन्दु है। (N, Y. z) का समुच्चय बिन्दु P की स्थिति का कार्तीय निर्देशांक (Cartesian coordinates) कहलाते हैं।

भौतिकी एवं अनुप्रयुक्त गणित में अनेक ऐसी समस्यायें होती है जहाँ कार्तीय निर्देशांकों का उपयोग सुविधाजनक नहीं होता है परन्तु भिन्न-भिन्न सममिति (symmetry ) के अनुसार निर्देश तंत्र का उपयोग करने से विश्लेषण सरल हो जाता है। इन सभी निर्देश तंत्रों को एक एकीकृत (unified) निर्देश तंत्र द्वारा परिभाषित किया जा सकता है। इस तंत्र को वक्र रेखी निर्देश (curvilinear coordinate system) कहते हैं ।

जैसा कि चित्र (1.1-2) में दर्शाया गया है कि वक्र रेखी निर्देश तंत्र तीन

वक्री पृष्ठों u1 = C1 (नियतांक), u2 = C2 (नियतांक) तथा u3 C3 (नियतांक ) से बनता है । किन्हीं दो पृष्ठों के प्रतिच्छेदन से बनने वाली वक्री रेखा निर्देशांक रेखा (curved coordinate line ) कहलाती है। वक्री पृष्ठ u1 = C1, u2 = C2 के प्रतिच्छेदन से बनने वाली निर्देशांक रेखा u3-वक्र कहलाती है। इसी प्रकार u2 = C2 व u3 = C3 प्रतिच्छेदन से u1 वक्र एवं u1= C1 u3 = C3 प्रतिच्छेद से 43-वक्र बनता U2 वक्र है। तीनों वक्री पृष्ठों का प्रतिच्छेदन बिन्दु मूल बिन्दु 0 कहलाता है। इस मूल बिन्दु O से इन u1. U2, u3 चक्र रेखाओं पर खींची गई स्पर्श रेखा निर्देशांक अक्ष (coordinate axis) कहलाती है।

इस बक्री-रेखी निर्देश तंत्र में किसी कण बिन्दु की स्थिति वक्र रेखी निर्देशांकों (u1, u2, u   3) के समुच्चय से दी जाती है जहाँ ये राशियाँ u1 = C1 (नियतांक), u2 = C2 (नियतांक) तथा u3 = C’3 (नियतांक) पृष्ठों का प्रतिच्छेद बिन्दु P है जहाँ कण की स्थित है।

लाम्बिक वक्र रेखी निर्देश तंत्र एवं स्केल गुणक (ORTHOGONAL CURVILINEAR COORDINATE SYSTEM AND SCALE FACTOR)

(यदि किसी वक्र रेखी निर्देशांक तंत्र में तीनों वक्री पृष्ठ u1 = C1 U2 = C2 तथा u3 = C3 परस्पर लम्बवत् है तो यह तंत्र लाम्बिक वक्र रेखी निर्देश तंत्र कहलाता है तथा इस निर्देश तंत्र में किसी बिन्दु के निर्देशांक लाम्बिक वक्र रेखी निर्देशांक (orthogonal curvilinear coordinates कहलाते हैं। अत: लाम्बिक निर्देश तंत्र में निर्देशांक परस्पर लम्बवत् होते हैं।

रेखा अल्पांश (Line element )

‘माना लाम्बिक वक्र रेखी निर्देश तंत्र में किसी बिन्दु के निर्देशांक (u1, u2, u3 ) है तो बिन्दु ‘P का स्थिति सदिश r ( u1, u2, u3 ) होगा-

वक्र रेखी निर्देश तंत्र में सदिश A

यदि लाम्बिक वक्र रेखी निर्देश तंत्र में u1, u2, u3 अक्षों के अनुदिश एकांक सदिश क्रमशः  तथा सदिश A के घटक A1, A2, A3 हो तो

 अदिश क्षेत्र की प्रवणता (GRADIENT OF A SCALAR FIELD) 

माना किसी अदिश क्षेत्र में दो समअदिश पृष्ठ S1 व S2 है जिन पर अदिश क्षेत्र का मान क्रमशः  है। अदिश राशि नियत होने के कारण पृष्ठ S1 के प्रत्येक बिन्दु पर समान है। इसी प्रकार अदिश राशि  पृष्ठ S2 पर नियत होने के कारण इसके प्रत्येक बिन्दु पर समान है।

माना पृष्ठ S1 के किसी बिन्दु P का स्थिति सदिश लाम्बिक वक्र रेखी निर्देशांक तंत्र के मूल बिन्दु O के सापेक्ष’r है तथा पृष्ठ S2 के किसी बिन्दु Q का स्थिति सदिश r + r  है। चित्र – (1.3-1). यदि बिन्दु P का लाम्बिक वक्ररेखी निर्देशांक तंत्र में निर्देशांक u1, u2, u3 है तो

R = r (u1, u2, u3)

बिन्दु P के सापेक्ष बिन्दु Q का विस्थापन PQ = r

तथा PQ की दिशा के अनुदिश अदिश फलन के परिवर्तन की दर 

पृष्ठों S1 व S2 के बीच न्यूनतम दूरी PR = n

फलन के अधिकतम् परिवर्तन की दर पृष्ठों के अभिलम्बवत् दिशा में होंगी। अतः

अत: अदिश क्षेत्र में अदिश फलन के अधिकतम परिवर्तन की दर को अदिश क्षेत्र  की प्रवणता कहते हैं।

अदिश क्षेत्र की प्रवणता सदिश राशि है तथा इसकी दिशा पृष्ठ के अभिलम्बवत् होती है। यदि समअदिश पृष्ठ के अभिलम्बवत् एकांक सदिश n  है तो

इस समीकरण का dr सदिश के साथ अदिश गुणनफल लेने पर,

चूँकि सभी लाम्बिक निर्देश तंत्रों में सदिश क्षेत्र के अदिश गुणनफल के गुण समान होते हैं, इसलिए

को अवकल संकारक कहते हैं। इसे प्राय: V (डेल) से व्यक्त किया जाता है।

सदिश क्षेत्र का डाइवर्जेन्स (DIVERGENCE OF A VECTOR FIELD) किसी सदिश क्षेत्र A में स्थिति आयतन अल्पांश को परिबद्ध करने वाले बन्द पृष्ठ से निर्गत प्रति एकांक आयतन सदिश फ्लक्स (flux) सदिश क्षेत्र का डाइवर्जेन्स (divergence) कहलाता है।

माना किसी अदिश क्षेत्र Ā में आयतन अल्पांश dV का बन्द पृष्ठ स्थित है। बन्द पृष्ठ से निर्गत फ्लक्स का मान है

अतः सदिश क्षेत्र A के आयतन अल्पांश की स्थिति पर डाइवर्जेन्स

माना लाम्बिक वक्र रेखी निर्देश तंत्र में किसी बिन्दु पर षटफलक आयतन अल्पांश dV स्थित है। इसके केन्द्रीय बिन्दु P के निर्देशांक (u1, u2, u3 ) हैं तथा इस पर सदिश क्षेत्र का मान Ā (u1, u2, u3 ) है। निर्देशांक अक्षों के अनुदिश सदिश क्षेत्र के क्रमशः A1,A2 तथा A3 है। यदि निर्देश तंत्र के निर्देशांक अक्षों के अनुदिश एकांक सदिश क्रमशः घटक e1, e2, e3 हो तो सदिश क्षेत्र

 सदिश क्षेत्र का कर्ल (CURL OF A VECTOR FIELD) माना सदिश क्षेत्र Ā’ में स्थित किसी बिन्दु P के चारों ओर एक काल्पनिक बन्द पथ है। बन्द पथ पर सदिश क्षेत्र Ā का समाकलन होता है-

जहाँ di बन्द पथ के अनुदिश रेखा अल्पांश है।

सदिश क्षेत्र के बन्द पथ पर रेखा समाकलन को प्राय: परिसंचरण (circulation) भी कहते हैं। रेखा समाकल बन्द पथ के द्वारा परिबद्ध के पृष्ठ तल अभिविन्यास पर निर्भर करता है। यदि बन्द पथ द्वारा परिबद्ध पृष्ठ तल को इस प्रकार रखा जाता है कि रेखा समाकल या परिसंचरण का मान अधिकतम हो जाये तो इस स्थिति में सदिश क्षेत्र का रेखा समाकल तथा बन्द पथ द्वारा परिबद्ध क्षेत्रफल के अनुपात का सीमान्त मान ( जब क्षेत्रफल शून्य के निकट हो) क्षेत्रफल अल्पांश की स्थिति पर परिमाण में सदिश क्षेत्र का कर्ल कहलाता है। अर्थात्

इसकी दिशा उस तल के लम्बवत् होती है जिसमें क्षेत्रफल अल्पांश की परिसीमा पर परिसंचरण अधिकतम् होता है। यदि क्षेत्रफल के लम्बवत् दिशा में एकांक सदिश हो, तो

लाम्बिक वक्र रेखी निर्देशांक तंत्र में किसी सदिश क्षेत्र का कर्ल या परिसंचरण ज्ञात करने के लिए इसके u1,u2, u3 घटकों के पृथक-पृथक व्यंजक प्राप्त करते हैं।

माना किसी बिन्दु O पर सदिश क्षेत्र Āके घटक A1, A2 तथा A, लाम्बिक वक्र रेखी निर्देशांक तंत्र के अक्षों के अनुदिश है। इस तंत्र का मूल बिन्दु O पर है।

अब कर्ल A के u3 घटक पर विचार करते हैं। जिसके लिए u3 अक्ष के लम्बवत् तल (u1) = नियतांक, u2-नियतांक) में स्थित क्षेत्रफल अल्पांश OLMN लेते हैं। यह क्षेत्रफल अल्पांश h1, du1, तथा h2 du2 रेखा अल्पांश से बना होता है जैसा कि चित्र (1.5-1) में दर्शाया गया है।

OL वक्र के अनुदिश सदिश क्षेत्र Ā का घटक = A1

हम जानते हैं कि बन्द पथ OLMNO के अनुदिश सदिश क्षेत्र Ā का समाकल उसकी भुजाओं के अनुदिश सदिश क्षेत्र के रेखा-समाकलों के योग के बराबर होता है। अतः

कर्ल की परिभाषानुसार किसी क्षेत्रफल अल्पांश को परिबद्ध करने वाले बंद परिपथ के अनुदिश सदिश क्षेत्र का रेखा – समाकल या परिसंचरण प्रति एकांक क्षेत्रफल पृष्ठ तल के लम्बवत् सदिश क्षेत्र के कर्ल के घटक के बराबर होता है। अतः

कर्ल A का u3 घटक

समीकरण (7) तथा (12) की तुलना करने पर,

curl A =  X A