clausius inequality in hindi theorem in thermodynamics derivation क्लासियस असमानता

क्लासियस असमानता क्या है क्लॉसियस प्रमेय किसे कहते हैं clausius inequality in hindi theorem in thermodynamics derivation ?

एन्ट्रोपी की ताप पर निर्भरता (Temperature Dependence of Entropy)

एन्ट्रोपी की ताप पर निर्भरता को एन्ट्रोपी की परिभाषा से बहुत ही सरल रूप में व्यक्त किया जा सकता है। माना कि कोई तंत्र ताप (T) तथा एक अन्य चरांक आयतन (V) अथवा दाब (P) का फलन है। उत्क्रमणीय रूपान्तरण में तंत्र की ऊष्माधारिता को निम्न प्रकार व्यक्त किया जा सकता है।

यहाँ (dqrev), तथा (dqrev)p क्रमशः स्थिर आयतन तथा स्थिर दाब पर अवशोषित ऊष्मा है। समीकरण (34) के अनुसार

dS = dqrev/T

समीकरण (34) तथा (83) द्वारा

इस प्रकार अवकलतथा के मान सम्बन्धित ऊष्मा धारिता के मानों को ताप से भाग देकर प्राप्त किया जा सकता है।

समीकरण (84) तथा (85) द्वारा ऊष्माधारिता की तुल्य परिभाषा दी जा सकती है।

उपरोक्त समीकरण एन्ट्रोपी की ताप पर निर्भरता को प्रदर्शित करती है।

(i) स्थिर आयतन पर ताप के साथ एन्ट्रोपी में परिवर्तन

समीकरण (84) के अनुसार

यदि तपT T1 से T2 हो जाए तो एन्ट्रोपी परिवर्तन होगा

यह मानते हुए कि इस ताप परिसर में Cv ताप पर निर्भर नहीं करता है तब

यदि पदार्थ के n मोल हो तो एन्ट्रोपी परिवर्तन

(ii) इसी प्रकार स्थिर दाब पर ताप के साथ एन्ट्रोपी परिवर्तन

क्लेशियस असमानता ( Classius Ineqality)

एन्ट्रोपी एक अवस्था फलन है जो तन्त्र की अवस्था पर निर्भर करती है अतः

यदि प्रक्रम चक्रीय हो तो प्रक्रम A से B पुनः B से A में आता है।

अर्थात् B से A जाने में एन्ट्रोपी परिवर्तन A से B जाने के लिए एस्ट्रोपी परिवर्तन के समान होगा लेकिन विपरीत चिन्ह वाला होगा तथा इन दोनों को जोड़ने पर शून्य होगा ।

यदि यह माना जाए कि पारिपार्श्विक से हमेशा ऊष्मा का स्थानान्तरण उत्क्रमणीय रूप से होता है

अतः किसी प्रक्रम की पारिपार्श्विक व तन्त्र की एन्ट्रॉपी में कुल परिवर्तन शून्य होगा। इससे यह निष्कर्ष निकाल सकते हैं कि उत्क्रमणीय प्रक्रम में एन्ट्रोपी का केवल तन्त्र व पारिवार्श्विक के मध्य स्थानान्तरण होता है व कुल एन्ट्रोपी परिवर्तन शून्य होता है।

लेकिन यदि प्रक्रम A – B में अनुत्क्रमणीय रूप से परिवर्तन होता है तो क्या होगा।

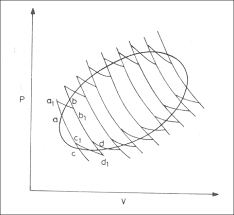
इस प्रक्रम की कोई भी प्रकृति हो लेकिन हम माने कि उत्क्रमणीय प्रक्रम B – A में परिवर्तन उत्क्रमणीय रूप से होता है तो इसको निम्न चक्र द्वारा प्रदर्शित करते हैं।

लेकिन अनुत्क्रमणीय चक्रीय प्रक्रम के लिए

यहाँ SAB प्रक्रम के A से B में जाने में एन्ट्रोपी परिवर्तन है। व्यंजक (95) को हम “क्लेसियस असमानता” कहते हैं जो कि वास्तविक बदलाव (Real transformation) के लिए आवश्यक आधार है तथा किसी अनुत्क्रमणीय बदलाव के लिए महत्वपूर्ण सम्बन्ध है समीकरण (95) की असमानता यह त करने में सहायक है कि बताया गया बदलाव प्रकृति में होगा या नहीं

(i) क्लेसियस असमानता का विलगित तन्त्र पर उपयोग (Clausius Inequality Applied to an isolated system) विलगित तंत्र के किसी परिवर्तन के लिए

dq (irrev) = 0

क्लेसियस असमानता समीकरण (95) का उपयोग करने पर

SAB > 0 या SAB = 0 ………………..(96)

अतः विलगित तंत्र में वास्तविक बदलाव के लिए ऐन्ट्रोपी S का मान धनात्मक चाहिए। अर्थात् विलगित तंत्र में स्वतः परिवर्तन (Natural change) के लिए प्रक्रम की एन्ट्रोपी बढ़ेगी। जब तक परिवर्तन चलता रहेगा एन्ट्रोपी का मान बढ़ता रहेगा तथा साम्यावस्था पर एन्ट्रोपी का मान अधिकतम होगा।

(ii) क्लेसियस असमानता का तन्त्र व पारिपार्श्विक पर उपयोग (Clausius Inequality Applied to System & Surroundings)

जहाँ समानता उत्क्रमणीय परिवर्तन को प्रदर्शित करता है जबकि असमानता अनुत्क्रमणीय परिवर्तन को प्रदर्शित करता है। लेकिन वास्तविक प्रक्रम (natural process) अनुत्क्रमणीय प्रकृति के होते हैं अतः इनकी एन्ट्रोपी बढ़ती है अर्थात् उत्क्रमणीय प्रक्रम में एन्ट्रोपी स्थिर रहती है जबकि अनुत्क्रमणीय प्रक्रम में एन्ट्रोपी बढती है। क्लेसियस ने इस प्रकार बताया की विश्व की ऊर्जा (Energy) तो स्थिर रहती हैं जबकि एन्ट्रोपी हमेशा बढ़ती है तथा अधिकतम की तरफ अग्रसर होती है। 2.21 आदर्श गैस के लिये एन्ट्रोपी परिवर्तन (Entropy changes for an Ideal Gas) माना की आदर्श गैस का एक तंत्र ताप T पर है, जिसका आयतन V तथा दाब P है। यह तंत्र अपने पारिपार्श्विक से dqrev ऊष्मा उत्क्रमणीय ढंग से अवशोषित करता है। इस प्रक्रम में एन्ट्रोपी परिवर्तन dS समीकरण (34) द्वारा दी जा सकती है।

ds = dqrev /T

चूंकि एन्ट्रोपी एक अवस्था फलन है अतः इसका मान तीन चरांको (P, V, T) में से किन्ही दो पर निर्भर करता है। इनमें से एक सामान्यतया ताप होता है दूसरे को आयतन (V) या दाब (P) लेकर आदर्श गैस के लिये एन्ट्रोपी परिवर्तन ज्ञात किया जाता है।

T तथा V को चरांक लिया जाता है- ऊष्मागतिकी के प्रथम नियम के अनुसार

प्रथम अवस्था में माना कि एन्ट्रोपी, आयतन तथा ताप क्रमश: S1, V1, तथा T1, है और द्वितीय अवस्था में क्रमशः S2, V2 तथा T2 है। एक परिमित अवस्था परिवर्तन में S तथा V में परिवर्तन (100) को दोनों अवस्थाओं की सीमाओं में समाकलित करके प्राप्त किया जा सकता है-

यदि ताप परास T1 से T2 के मध्य Cv का मान स्थिर माना जाये तो

T तथा P को चरांक लिया जाता है

यदि प्रथम अवस्था में गैस का दाब P1 तथा द्वितीय अवस्था में गैस का दाब P2 हो तो आदर्श गैस समीकरण के अनुसार

यदि तंत्र में आदर्श गैस के n मोल हो तो

समीकरण ( 101 ) तथा ( 105) से स्पष्ट है कि आदर्श गैस के लिये एन्ट्रोपी परिवर्तन प्रारम्भिक एवं अन्तिम अवस्था पर निर्भर करता है।

आदर्श गैस के विभिन्न प्रक्रमों में एन्ट्रोपी परिवर्तन

समीकरण (102) तथा (105) का उपयोग करके विभिन्न प्रक्रमों जैसे समतापी प्रक्रम, समदाबी प्रक्रम समआयतनिक प्रक्रम आदि में एन्ट्रोपी परिवर्तन की गणना की जा सकती है।

(i) समतापी प्रक्रम (Isothermal Proccess):- समतापी प्रक्रमों में ताप स्थिर रहता है अर्थात् T1 = T2 यदि ST स्थिर ताप पर एन्ट्रोपी परिवर्तन हो तो समीकरण (104) तथा ( 105 ) निम्न प्रकार लिखी जा सकती है।

गैस के प्रसार में (जबकि V2 > V1 या P1 > P2) एन्ट्रोपी परिवर्तन धनात्मक तथा सम्पीडन में (जबकि V2 < V1 या P1 <P2) में एन्ट्रोपी परिवर्तन ऋणात्मक होता है इससे यह निष्कर्ष निकलता है कि समतापी प्रसार में एन्ट्रोपी बढ़ती है जबकि समतापी सम्पीडन में एन्ट्रोपी घटती है ।

(ii) समदाबी प्रक्रम (Isobaric Process) – समदाबी प्रक्रम में दाब स्थिर रहता है, अर्थात् P1 = P2 यदि Sp स्थिर दाब पर एन्ट्रोपी परिवर्तन हो तो समीकरण (105) द्वारा

समीकरण (98) से स्पष्ट है कि स्थिर दाब पर ताप बढ़ाने से आदर्श गैस की एन्ट्रोपी बढ़ती है।

(iii) समआयतनिक प्रक्रम (Isochoric Process) – समआयतनिक प्रक्रम में आयतन स्थिर रहता है अर्थात् V1 = V2 यदि Sv स्थिर आयतन पर एन्ट्रोपी परिवर्तन हो तो समीकरण (105) द्वारा

आदर्श गैसों के मिश्रण की एन्ट्रोपी (Entropy of a Mixture of Ideal Gases)

जैसा कि पहले बताया जा चुका है एक मोल आदर्श गैस के लिये

Cv का मान स्थिर मानते हुये समाकलन करने पर

यदि तंत्र आदर्श गैसों का मिश्रण हो तो मिश्रण की एन्ट्रोपी प्रत्येक गैस की एन्ट्रोपी के योग के बराबर होगी। यदि n1. n2. n3……. …गैसों के मोल तथा P1. P2. P.3…… एन्ट्रोपी निम्न व्यंजक द्वारा लिखी जा सकती है।

इस प्रकार समीकरण (114) आदर्श गैस के मिश्रण की एन्ट्रोपी प्रदर्शित करती है।

मिश्रित करने में एन्ट्रोपी परिवर्तन (Entropy of Mixing or Entrpy change in Mixing)

दाब P पर गैसों के मिश्रण की एन्ट्रोपी तथा उसी दाब पर प्रत्येक गैस की एन्ट्रोपी के योग का अन्तर, मिश्रित करने में एन्ट्रोपी परिवर्तन कहलाता है अर्थात्

S मिश्रण = दाब P पर गैसों के मिश्रण की एन्ट्रोपी – दाब P पर प्रत्येकगैस की एन्ट्रोपी का योग

यहाँ ni तथा xi क्रमशः मिश्रण में अवयवी गैसों के मोल की संख्या तथा उनकी मोल भिन्न है । मान लीजिए कि मिश्रण में कुल मोलों की संख्या n है

अतः एक मोल गैसीय मिश्रण के लिए S मिश्रण का मान निम्न समीकरण द्वारा लिखा जा सकता

चूंकि xi हमेशा भिन्न में होगा अतः S मिश्रण का मान हमेशा धनात्मक होगा ।