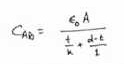Sbistudycapacitance of spherical capacitor in hindi , संधारित्र का सिद्धांत :-
गोलाकार चालक की धारिता : R त्रिज्या के धातु के गोले के पृष्ठ पर वितरित आवेश q है , जैसे जैसे गोले को आवेशित करते है , इसके विभव वृद्धि होती है। आवेशित चालक गोले की धारिता –
C = q/V …..समीकरण-1
गोले के पृष्ठ पर विद्युत विभव –
V = kq/R …..समीकरण-2
समीकरण-2 से मान समीकरण-1 में रखने पर –
C = R/k
चूँकि k = 1/4πE0
C = R/(1/4πE0)
C = 4πE0R
C ∝ R
अत: स्पष्ट है कि गोले की त्रिज्या बढाने पर धारिता बढती है अत: धारिता चालक के आकार पर निर्भर करती है।
धारिता (C) व गोले की त्रिज्या (R) के मध्य सीधी रेखा प्राप्त होती है।
यदि गोले का आकार पृथ्वी के आकार के बराबर हो –
R = Re = 6400 Km = 6400 x 10+3 m
C = 4πE0Re
C = 4 x 3.14 x 8.85 x 10-12 x 6400 x 10+3
C = 711 uF
संधारित्र : संधारित्र एक ऐसी विद्युत युक्त है जिसके आकार में बिना परिवर्तन किये बिना आवेश धारण की क्षमता बढाई जाती है।
संधारित्र की दोनों प्लेटो पर आवेश का परिमाण समान एवं प्रकृति विपरीत होती है। फलस्वरूप संधारित्र का कुल आवेश शून्य होता है।
किसी संधारित्र की धारिता आवेश को धारण करने की क्षमता होती है।
संधारित्र का सिद्धांत
संधारित्र के प्रकार
तीन प्रकार के है –
3. बेलनाकार संधारित्र
1. समान्तर प्लेट संधारित्र व इसकी धारिता : समान्तर प्लेट संधारित्र में समान धातु की बनी समान क्षेत्रफल की दो प्लेटे अल्प दूरी पर व्यवस्थित होती है।
प्लेट A पर जितना धनावेश उपस्थित होता है। प्लेट B की आंतरिक सतह पर उतना ही ऋण आवेश उपस्थित होता है। प्लेट B की बाहरी सतह को भू-सम्पर्कित रखते है।
संधारित्र की दोनों प्लेटों के मध्य एक समान विद्युत क्षेत्र उत्पन्न होता है।
चालक प्लेट A के कारण बिंदु P पर विद्युत क्षेत्र की तीव्रता –
E1 = σ/2E0 समीकरण-1
चूँकि σ = प्लेट का पृष्ठीय आवेश घनत्व है।
चालक प्लेट B के कारण बिंदु P पर विद्युत क्षेत्र की तीव्रता –
E2 = σ/2E0 समीकरण-2
बिंदु P पर कुल विद्युत क्षेत्र की तीव्रता –
E = E1 + E2
E = σ/2E0 + σ/2E0
E = σ/E0 समीकरण-3
यदि समान्तर प्लेट संधारित्र की प्लेटों का क्षेत्रफल A व दोनों प्लेटो के मध्य की दूरी d हो तो निर्वात की स्थिति में संधारित्र की धारिता C = Aε0/d समीकरण-1
यदि प्लेटो के मध्य d दूरी में पूर्ण रूप से ε0 परावैधुत उपस्थित हो तो संधारित्र की धारिता C’ = Aε/d समीकरण-2
माध्यम का परावैद्युत εr = ε/ε0
अतः ε = εr ε0 समीकरण-3
समीकरण-2 से
C’ = A εrε0/d
C’ = C εr
अत: स्पष्ट है कि माध्यम की उपस्थिति में धारिता εr गुना बढ़ जाती है।
समान्तर प्लेट संधारित्र की धारिता (जब प्लेटों के मध्य आंशिक रूप से परावैद्युत माध्यम उपस्थित हो) :
किसी समान्तर प्लेट संधारित्र की d दूरी पर व्यवस्थित प्लेटो के मध्य t मोटाई का परावैद्युत माध्यम उपस्थित है।
परावैधुत माध्यम को विद्युत क्षेत्र E में रखते है तो इसके अणु ध्रुवित हो जाते है , फलस्वरूप परावैद्युत माध्यम की एक सतह ऋण आवेशित व दूसरी सतह धनावेशित होने से माध्यम के अन्दर उत्पन्न विद्युत क्षेत्र Et बाह्य विद्युत क्षेत्र को कम करने का प्रयास करता है।
समान्तर प्लेट संधारित्र की प्लेटो के मध्य विभवान्तर V = V1 + V2
V1 = (d – t ) मोटाई अर्थात निर्वात में विभवान्तर
V2 = t मोटाई में अर्थात माध्यम में विभवान्तर
संधारित्र की धारिता –
