BESSEL DIFFERENTIAL EQUATION in hindi in physics बेसल अवकल समीकरण का व्यापक हल का सूत्र क्या है
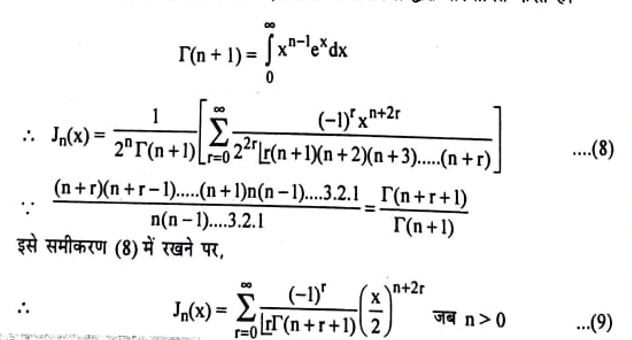
बेसल अवकल समीकरण का व्यापक हल का सूत्र क्या है BESSEL DIFFERENTIAL EQUATION in hindi in physics ?
बेसल अवकल समीकरण ( BESSEL DIFFERENTIAL EQUATION)
निम्न द्वितीय कोटि का रैखिक अवकल समीकरण
को n कोटि का बेसल समीकरण कहते हैं तथा इसका हल n कोटि का बेसल फलन कहलाता है। इसमें x = 0 परpo(x) = x2 = 0 अर्थात् शून्य प्राप्त होता है। अतः बेसल अवकल समीकरण का विचित्र बिन्दु x = 0 है।
विचित्र बिन्दु x = 0 पर,
अतः बेसल समीकरण का नियमित विचित्र बिन्दु x = 0 है इसलिये इस बिन्दु के निकट इसका हल प्राप्त कर सकते हैं। माना बेसल समीकरण का हल निम्न घात श्रेणी है।
इसका अवकलन करने पर,
इन अवकलजों को समीकरण (1) में रखने पर,
चूँकि समीकरण (2) अवकल समीकरण (1) का हल है इसलिये समीकरण ( 3 ) x के प्रत्येक मान के लिये संतुष्ट होनी चाहिये। अत: यह एक तत्समक (identity) है इसलिये इसमें x के प्रत्येक घात वाले पद में गुणांक अलग-अलग शून्य होना आवश्यक है। अतः समीकरण (3) में xm+r के गुणांक को शून्य के बराबर करने पर,
यह एक पुनरावृत्ति सूत्र है जिसके द्वारा सभी गुणांकों को ज्ञात कर सकते हैं। यदि हम = 0 रखें तो
चूँकि घात श्रेणी Ao से प्रारम्भ होती है इसलिये हम A2 = 0 रख सकते हैं। इस प्रकार निम्न घातांकी समीकरण (indicial equation) प्राप्त होती है।
अतः m के दो मान होने के कारण बेसल समीकरण के दो हल होते हैं। परिस्थिति I: जब m=n
समीकरण (4) में m = n रखने पर,
A_1=A_2=A_3= 0 ध्यान में रखते हुए इसमें r = 1, 3, 5 …. रखते हैं।
पुन: A_1= A2 =A_3 = 0 ध्यान में रखते हुए समीकरण ( 5 ) में r = 0, 2, 6 …. रखते हैं।
चूँकि श्रेणी Ag से प्रारम्भ होती है इसलिये इसका मान ज्ञात नहीं किया जा सकता है और नही यह शून्य के बराबर होता है ।
इन गुणांकों को समीकरण (2) में रखने पर बेसल अवकल समीकरण का एक हल निम्न श्रेणी रूप में प्राप्त हो जाता है।
‘जब नियतांक A0 को विशिष्ट मान दिया जाता है तो हल y1 को कोटि n का प्रथम प्रकार का बेसल फलन Jn(x) कहते हैं। Ao का विशिष्ट मान है :
जहाँ I गामा फलन कहलाता है तथा इसको निम्न समाकल द्वारा परिभाषित करते हैं।
परिस्थिति II : जब m =-n
बेसल समीकरण का दूसरा हल समीकरण (9) में n को -n से प्रतिस्थापित करके प्राप्त किया जा सकता है। अतः बेसल समीकरण के दूसरे हल को कोटि-n का प्रथम प्रकार का बेसल फलन J-n(x) कहते हैं।
यह प्रदर्शित किया जा सकता है कि यदि ॥ धनपूर्णाक नहीं है तो Jn(x) तथा J-n(x) स्वतंत्र फलन होते हैं। ऐसी स्थिति में बेसल समीकरण का व्यापक हल होगा।
y = AJn(x) + BJ_n(x) n पूर्णांक……………..(11)
यह ध्यान देने योग्य बात है कि जब n धनपूर्णांक होता है कि Jn (x) तथा Jn (x) स्वतंत्र फलन नहीं होते हैं तथा वे निम्न समीकरण द्वारा सम्बन्धित होते हैं, यह उदाहरण (8) में सिद्ध किया गया है।
J_n(x) = (-1)nJn(x)……………(12)
जहाँ n धनपूर्णांक होने पर गामा फलन क्रमगुणित ( factorial) में बदला जा सकता है।
इस स्थिति में बेसल समीकरण का दूसरा हल दूसरे प्रकार का बेसल फलन कहलाता है। इस विशिष्ट हल को न्यूमान फलन (Neumann function) कहते हैं। इसे Nn या Yn से व्यक्त करते हैं। अतः n के धनपूर्णाक होने की स्थिति में बेसल समीकरण का व्यापक हल होगा।
y = CJn (x) + DNn (x)………………….(15)
सीमांत परिस्थिति में जब x – 0 हो तो Nn – 0 तथा y – 0 अतः समीकरण ( 15 ) में गुणांक D शून्य होगा एवं
(7.12Jn (x) का उदभव फलन (GENERATING FUNCTION OF Jn (x))
जब फलन exp [x(z-1/z)/2] को z के घातों के बढ़ते हुए तथा घटते हुए क्रम में श्रेणी रूप में विस्तारित किया जाय तो यह प्रथम प्रकार के बेसल फलन को उत्पन्न करता है।
इस समीकरण में zn के गुणांकों को एकत्रित करने पर,
इसी प्रकार इस समीकरण में zn के गुणांकों को एकत्रित करने पर,
समीकरण (2) तथा (3) को संयुक्त करने पर,
7.13 J(x) an ariqft (RECURRENCE RELATIONS FOR Jn(x))
बेसल फलन के श्रेणी से,
बेसल फलन को x के सापेक्ष अवकलन करने पर,
दूसरी श्रेणी में r = (k+ 1) रखने पर,
बेसल फलन के श्रेणी से,
बेसल फलन को x के सापेक्ष अवकलन करने पर,
इसे x से गुणा करने पर,
सम्बन्ध (1) तथा (2) का योग करने पर,
इस समीकरण के दोनों तरफ xn से गुणा करके x के सापेक्ष समाकल करने पर,
हिंदी माध्यम नोट्स
Class 6
Hindi social science science maths English
Class 7
Hindi social science science maths English
Class 8
Hindi social science science maths English
Class 9
Hindi social science science Maths English
Class 10
Hindi Social science science Maths English
Class 11
Hindi sociology physics physical education maths english economics geography History
chemistry business studies biology accountancy political science
Class 12
Hindi physics physical education maths english economics
chemistry business studies biology accountancy Political science History sociology
English medium Notes
Class 6
Hindi social science science maths English
Class 7
Hindi social science science maths English
Class 8
Hindi social science science maths English
Class 9
Hindi social science science Maths English
Class 10
Hindi Social science science Maths English
Class 11
Hindi physics physical education maths entrepreneurship english economics
chemistry business studies biology accountancy
Class 12
Hindi physics physical education maths entrepreneurship english economics