WhatsApp Group Join Now

Telegram Join Join Now

प्रकाश का वर्ण विक्षेपण , कोणीय वर्ण विक्षेपण , क्षमता , प्रकाश का प्रकीर्णन , रेले का नियम Angular Dispersion and Dispersive Power in Hindi

SbistudyJanuary 19, 2020inPhysics

Angular Dispersion and Dispersive Power in Hindi , प्रकाश का वर्ण विक्षेपण , कोणीय वर्ण विक्षेपण , क्षमता , प्रकाश का प्रकीर्णन , रेले का नियम :-

प्रिज्म (prism in hindi) : जब किसी पारदर्शी व समांग माध्यम को तीन आयताकार व दो त्रिभुजाकार अपवर्तक पृष्ठों के मध्य भर दिया जाए तो इसे व्यवस्था को प्रिज्म कहते है।

प्रिज्म के दोनों अपवर्तक पृष्ठों के मध्य बने कोण को प्रिज्म कोण कहते है।

प्रिज्म के जिन पृष्ठों से प्रकाश किरण प्रवेश करके बाहर निकलती है उन्हें प्रिज्म के अपवर्तक पृष्ठ कहते है।

अपवर्तक पृष्ठ के अलावा शेष आयताकार पृष्ठ को प्रिज्म का आधार पृष्ठ कहते है।

प्रिज्म में आपतित किरण की दिशा व निर्गत किरण की दिशा के मध्य बने कोण को प्रिज्म का विचलन कोण कहते है।

प्रिज्म का अपवर्तनांक ज्ञात करने के लिए :-

∠PQN₁ = i₁ आपतन कोण (AB अपवर्तक पृष्ठ पर)

∠RQU = r₁अपवर्तन कोण (AB अपवर्तक पृष्ठ पर)

∠QRU = r₂ आपतन कोण (AC अपवर्तक पृष्ठ पर)

∠SRN₂ = i₂अपवर्तन कोण (निर्गत कोण) (AC अपवर्तक पृष्ठ पर)

समांतर चतुर्भुज AQUR से –

∠RAQ + ∠AQU + ∠QUR + ∠URA = 360

A + 90 + ∠QUR + 90 = 360

∠QUR = 180 – A समीकरण-1

त्रिभुज △QUR से –

∠RQU + ∠QUR + ∠URQ = 180

r₁ + ∠QUR + r₂ = 180

∠QUR = 180 – (r₁+ r₂) समीकरण-2

समीकरण-1 व समीकरण-2 की तुलना करने पर –

180 – (r₁+ r₂) = 180 – A

r₁+ r₂ = A समीकरण-3

त्रिभुज △TQR से –

∠VTR = ∠TQR + ∠QRT (बहिर्कोण)

ς = ( i₁ – r₁) + (i₂ – r₂)

ς = ( i₁+i₂) – (r₁ + r₂) समीकरण-4

समीकरण-3 का मान समीकरण-4 में रखने पर –

ς = i₁+i₂ – A

ς + A = i₁+i₂समीकरण-5

न्यूनतम विचलन कोण के लिए यह आवश्यक शर्त है कि-

i₁= i₂ = i तथा r₁ = r₂ = r होना चाहिए।

इसलिए समीकरण-5 से –

r + r = A

2r = A

r = A/2 समीकरण-6

इसी प्रकार समीकरण-5 से –

i + i = ς_min + A

2i = ς_min + A

i = (ς_min + A)/2 समीकरण-6

स्नेल नियम से –

u₂₁ = sin i/sin r समीकरण-8

[u₂₁ = u₂/u₁ = u/1 = u]

समीकरण-6 व समीकरण-7 के मान समीकरण-8 में रखने पर –

u = {sin(ς_min + A)/2}/{sin(A/2)}

यही प्रिज्म सूत्र है।

पतले प्रिज्म के लिए sinθ = θ के बराबर है ,

इसलिए

sin(ς_min + A)/2 = (ς_min + A)/2 तथा sin A/2 = A/2 होगी।

अत: u = {(ς_min + A)/2}/(A/2)

u = ς_min + A/A

u = ς_min/A + 1

ς_min = (u – 1)A

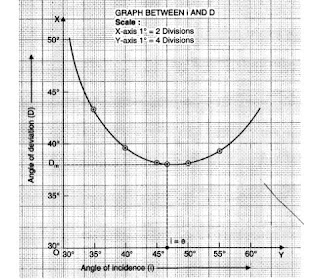
विचलन कोण (ς) व आपतन कोण (i) के लिए मध्य ग्राफ –

प्रकाश का वर्ण विक्षेपण

जब कोई प्रकाश किरण अपने अवयवी रंगों में विभाजित होती है तो प्रकाश की इस घटना को प्रकाश का वर्ण विक्षेपण कहते है।

प्रिज्म द्वारा प्रकाश का वर्ण विक्षेपण।

जब किसी प्रकाश किरण को प्रिज्म से गुजारते है तो निर्गत प्रकाश में विभिन्न रंगों का समूह प्राप्त होता है जिसे प्रकाश का वर्ण क्रम कहते है।

प्रिज्म से निर्गत प्रकाश में प्राप्त होने वाले रंग क्रमशः बैंगनी , जामुनी , नीला , हरा, पीला , नारंगी व लाल (VIBGYOR) प्राप्त होता है।

कोणीय वर्ण विक्षेपण (θ) : जब किसी प्रकाश किरण को प्रिज्म से गुजारते है तो प्रिज्म से प्राप्त होने वाले रंगों में सीमांत रंगों के विचलन कोण के अंतर को ही कोणीय वर्ण विक्षेपण कहते है।

अथवा

बैंगनी रंग व लाल रंग के विचलन कोणों का अंतर ही कोणीय वर्ण विक्षेपण कहलाता है अर्थात कोणीय वर्ण विक्षेपण –

θ = ξ_v – ξ_R

θ = (u_v -1)A – (u_R – 1)A

θ = (u_v – u_R)A

कोणीय विक्षेपण क्षमता (w) : प्रकाश के वर्ण विक्षेपण में कोणीय विक्षेपण तथा माध्य रंग के विचलन कोण के अनुपात को ही कोणीय विक्षेपण क्षमता कहते है।

अर्थात

कोणीय विक्षेपण क्षमता w = θ/ξ_y

अथवा

w = (ξ_v – ξ_R)/ξ_y

या

w = (ξ_v – ξ_R)/(ξ_y-1)

जब कोई प्रकाश किरण ऐसे अणु पर आपतित होती है जिसका आकार आपतित प्रकाश की तरंग दैर्ध्य से कम हो तो अणु पहले प्रकाश का अवशोषण करता है उसके पश्चात् संभव सभी दिशाओ में उसे फैलाता है तो प्रकाश की इस घटना को ही प्रकाश का प्रकीर्णन कहते है।

रैले का नियम

रेले के नियम के अनुसार प्रकिर्णित प्रकाश की तीव्रता आपतित प्रकाश की तरंग दैर्ध्य की चतुर्थ घात के व्युत्क्रमानुपाती होती है।

अर्थात

I_S ∝ 1/ λ⁴

जिस प्रकाश की तरंग दैधर्य जितनी अधिक होती है वह प्रकाश उतना ही कम प्रकिर्णित होता है तथा जिस प्रकाश की तरंग दैधर्य जितनी कम होती है , वह प्रकाश उतना ही अधिक प्रकिर्णित होती है अर्थात लाल रंग का प्रकीर्णन सबसे कम तथा बैंगनी रंग का प्रकीर्णन सबसे अधिक होता है।

यदि अणु का आकार आपतित प्रकाश की तरंग दैधर्य से कम हो तो प्रकाश प्रकिर्णित होगा परन्तु यदि अणु का आकार आपतित प्रकाश की तरंग दैधर्य से अधिक हो तो या तो प्रकाश प्रकिर्णित नहीं होगा या फिर सभी प्रकाश समान रूप से प्रकिर्णित होंगे।

प्रकाश के प्रकीर्णन से सम्बन्धित कुछ महत्वपूर्ण घटनाएँ :

1. सूर्योदय व सूर्यास्त के समय सूर्य का लाल दिखाई देना : सूर्योदय व सूर्यास्त के समय सूर्य पृथ्वी से अधिक दूरी पर होता है। सूर्य से आने वाली प्रकाश किरणें वायुमंडल के अणुओं से प्रकिर्णित हो जाती है। लाल रंग की तरंग दैधर्य अधिक होने के कारण इसका प्रकीर्णन कम होता है , जिसके कारण यह अधिक दूरी तय करता हुआ प्रेक्षक की आँखों में पहुँचता है इसलिए सूर्योदय व सूर्यास्त का समय सूर्य लाल रंग का दिखाई देता है।

2. स्वच्छ आकाश का नीला दिखाई देना : सूर्य से आने वाली प्रकाश किरणों का वायुमंडल के अणुओं द्वारा प्रकीर्णन होता है।

बैंगनी , जामुनी व नीले रंग का प्रकीर्णन अधिक होता है परन्तु नीले रंग के प्रति आँखें संवेदनशील होने के कारण आकाश नीला दिखाई देता है।

3. अन्तरिक्ष या वायुयान में स्थित व्यक्ति को अन्तरिक्ष का काला दिखाई देना : सूर्य से आने वाली किरणों का अन्तरिक्ष में उपस्थित अणुओं से प्रकीर्णन होता है। बैंगनी रंग व जामुनी रंग का प्रकीर्णन सर्वाधिक होने के कारण अन्तरिक्ष या वायुयान में स्थित व्यक्ति को अन्तरिक्ष काला दिखाई देता है।

4. बादलों का रंग सफ़ेद दिखाई देना : सूर्य से आने वाली किरणें जब बादलो से टकराती है तो बादलो का आकार आपतित प्रकाश की तरंग दैधर्य से बहुत अधिक होने के कारण सभी रंगों का प्रकीर्णन समान रूप से होता है इसलिए बादल सफ़ेद दिखाई देते है।

5. खतरे के निशान लाल रंग के बनाना : लाल रंग की तरंग दैधर्य सबसे अधिक होने के कारण इसका प्रकीर्णन सबसे कम होता है।

इसलिए लाल रंग अधिक दूरी तय करता हुआ प्रेक्षक की आँखों में पहुँचता है इसलिए खतरे के निशान लाल रंग के बनाये जाते है।