DIFFUSION EQUATION HEAT CONDUCTION IN THIN RECTANGLE PLATE in hindi विसरण समीकरण क्या है
विसरण समीकरण क्या है DIFFUSION EQUATION HEAT CONDUCTION IN THIN RECTANGLE PLATE in hindi ?
विसरण समीकरणः पतली आयताकार प्लेट में उष्मा प्रवाह (DIFFUSION EQUATION: HEAT CONDUCTION IN THIN RECTANGLE PLATE) जब कभी उष्मा चालक माध्यम में किन्हीं दो बिंदुओं के बीच तापांतर होता है तो उच्च ताप क्षेत्र से निम्न ताप क्षेत्र की ओर उष्मा प्रवाह होता है। उष्मा प्रवाह की दर उनके तापातर के समानुपाती होती है। उष्मा चालक माध्यम के किसी बिंदु पर ताप ज्ञात करने के लिये निम्न उष्मा प्रवाह समीकरण (heat flow quation) का उपयोग करते हैं। इस समीकरण को विसरण समीकरण (diffusion equation) भी कहते हैं-
जहाँ h2=K/pC माध्यम की उष्मीय विसरणता ( thermal diffusivity) कहलाती है, K उष्मा चालकता (thermal conductivity) गुणांक, p घनत्व ( density) तथा C विशिष्ट उष्मा (specific heat) है।
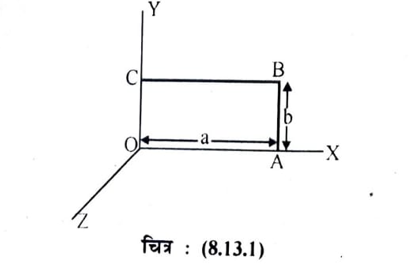
उष्मा प्रवाह समीकरण को हल करने के लिये उदाहरण के तौर पर, a लम्बाई व b चौड़ाई की एक पतली आयताकार प्लेट लेते है जिसके किनारे x = 0, x = a, y ‘ = 0 तथा y = b पर ताप शून्य रहता है तथा प्रारम्भ मे अर्थात 1 = 0 पर प्लेट पर कहीं भी ताप शून्य नहीं होता है।
चूंकि प्लेट पतली है तथा आकार में आयताकार है इसलिये उष्मा प्रवाह एक तल में माना जा सकता है तथा उष्मा प्रवाह समीकरण को द्विविमीय कार्तीय निर्देशांकों (xy) में लिख सकते हैं- होंगे। होंगे
माना इस समीकरण का हल है-
………………….(3)
इस समीकरण को समीकरण (2) में रखकर X(x) Y(y) T(t) से भाग देने पर
इस समीकरण के तीनों पद एकल चर फलन है इसलिये ये सभी किसी नियतांक के बराबर माना ये नियतांक क्रमशः –kx2 – ky2 तथा – k0/h2 है।
समीकरण (5) को समीकरण (4) में रखने पर हम नियतांकों में निम्न संबंध प्राप्त करते हैं।
समीकरण (Sc) को हल करने पर.
अत: प्लेट का ताप समय के सापेक्ष चर घातांकी रूप से कम होता है।
समीकरण (5a) तथा (5b) सरल आवृतिक दोलक के समीकरण के समतुल्य है अतः इनके हल
नियतांकों A, B, C, D, kx तथा ky को इस समस्या के परिसीमा प्रतिबंधों द्वारा ज्ञात किया जा सकता है।
(i) प्लेट के किनारे x = 0 पर ताप 0 = 0 या X (x) = 0 होता है अतः समीकरण (8) से,
ये मान समीकरण (8) में रखने पर,
इसी प्रकार प्लेट के किनारे y = 0 पर ताप 0 = 0 या Y (y) = 0 होता है । अत: समीकरण (9) से,
ये मान समीकरण (9) में रखने पर,
समीकरण ( 7 ), ( 10 ) व ( 11 ) को समीकरण (3) में रखने पर,
चूंकि किसी बिंदु (x,y) पर ताप 6 (x, y,t),m व n के सभी मानों के लिये वैध है इसलिये उष्मा प्रवाह समीकरण का व्यापक हल होगा-
जहाँ_Amn = ABD तथा समीकरण (6) से
अब अज्ञात नियतांक Amp को समस्या के प्रारम्भिक ताप द्वारा ज्ञात करते
इस प्रतिबंध को समीकरण ( 12 ) में आरोपित करने पर,
इस समीकरण को
से गुणा कर तथा 0 व a व b के बीच समाकलन करने पर,
गुणांक Amn का मान समीकरण (12) में रखने पर पतली प्लेट के लिये उष्मा प्रवाह समीकरण का पूर्ण व्यापक हल प्राप्त हो जाता है।
यदि प्लेट मोटी है तो इस समस्या का हल ज्ञात करने के लिये त्रिविमीय कार्तीय निर्देशांकों में ऊष्मा प्रवाह समीकरण का उपयोग करते हैं-
पहले वाली प्रक्रिया का अनुसरण करके इस समीकरण का निम्न हल लिख सकते है।
जहाँ c मोटी प्लेट की मोटाई है,
हिंदी माध्यम नोट्स
Class 6
Hindi social science science maths English
Class 7
Hindi social science science maths English
Class 8
Hindi social science science maths English
Class 9
Hindi social science science Maths English
Class 10
Hindi Social science science Maths English
Class 11
Hindi sociology physics physical education maths english economics geography History
chemistry business studies biology accountancy political science
Class 12
Hindi physics physical education maths english economics
chemistry business studies biology accountancy Political science History sociology
English medium Notes
Class 6
Hindi social science science maths English
Class 7
Hindi social science science maths English
Class 8
Hindi social science science maths English
Class 9
Hindi social science science Maths English
Class 10
Hindi Social science science Maths English
Class 11
Hindi physics physical education maths entrepreneurship english economics
chemistry business studies biology accountancy
Class 12
Hindi physics physical education maths entrepreneurship english economics