लॉप्लास समीकरण LAPLACE EQUATION IN TWO DIMENSIONAL in hindi लाप्लास का समीकरण
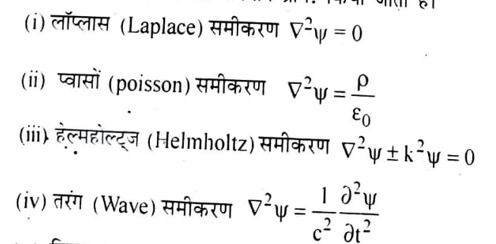
लाप्लास का समीकरण को समझाइए लॉप्लास समीकरण LAPLACE EQUATION IN TWO DIMENSIONAL in hindi ?
अध्याय : परिसीमा मान समस्याऐं (Boundary Value Problems)
प्रस्तावना (INTRODUCTION)
यह सर्वविदित है कि गणितीय भौतिकी की अधिकांश परिघटनाओं (phenomena) को परिसीमा समस्याओं की सहायता से हल करके समझाया जा सकता है। परिसीमा समस्याओं (boundary problems) में अधिकांशत: परिसीमा प्रतिबंध (boundary conditions) सहित द्वितीय कोटि के आंशिक अवकल समीकरणें प्राप्त होती है जिनके हल से उस भौतिक राशि का मान ज्ञात किया जा सकता है। आंशिक अवकल समीकरणों वे समीकरणें होती है जिनमें दो या दो अधि क चर राशियों पर निर्भर अज्ञात फलन व उसके अवकलजों में संबंध होता है। अत: परिसीमा मान समस्या का हल भौतिक समस्या से सम्बंधित आंशिक अवकलन समीकरण का हल होता है। जो उस समस्या की परिसीमा प्रतिबंधों द्वारा संतुष्ट होता है ।
भौतिकी की अनेक शाखाओं में वं समस्याएं जो तरंग समीकरण, उष्मा प्रवाह, विद्युत एवं चुम्बकीय क्षेत्रों का वितरण काण्टम यांत्रिकी परिघटना आदि से सम्बन्धित होती है तथा परिसीमा पृष्ठ से प्रतिबंधित होती है। उन्हें प्रायः परिसीमा मान समस्या कहा जाता है।.
यद्यपि द्वितीय कोटि के आंशिक अवकल समीकरण हल करने की अनेक विधियाँ है परन्तु इस अध्याय में हम केवल एक महत्वपूर्ण विधि का उपयोग करेंगे जिसे चरों का पृथक्करण (separation of variables) तकनीक कहते हैं। इसके द्वारा बहुचर आंशिक अवकल समीकरण में एकल चर अवकल समीकरणों को पृथक किया जाता है।
भौतिकी परिघटनाओं की समस्याओं को हल करने के लिए निम्न कुछ आंशिक अवकल समीकरण दिये गये है जिनका उपयोग प्राय: किया जाता है।
(v) विरसण या ऊष्मा प्रवाह (Diffusion or Heat flow) समीकरण
(vi) काल निर्भर श्रोडिंजर समीकरण (Time dependent Schrodinger equation)
द्विविमीय कार्तीय निर्देशांकों में लॉप्लास समीकरण (LAPLACE EQUATION IN TWO DIMENSIONAL CARTESIAN COORDINATES) परिसीमा से बंधी अधिकांश भौतिक समस्याओं जैसे द्रव्य रहित क्षेत्र में गुरूत्वीय विभव का वितरण, आवेश रहित क्षेत्र में स्थिर विद्युत क्षेत्र का वितरण, धारा रहित क्षेत्र में स्थिर चुम्बकीय क्षेत्र का वितरण, उष्मा स्रोत रहित क्षेत्र में स्थायी अवस्था में ताप वितरण ज्ञात करने में लॉप्लास समीकरण का उपयोग किया जाता है। लॉप्लास समीकरण को निम्न समीकरण से व्यक्त किया जाता है।
इस समीकरण का हल स्वतंत्र चर राशियों की संख्या तथा निर्देश तंत्र के स्वरूप ( कार्तीय या बेलनाकार या गोलीय निर्देश तंत्र) पर निर्भर करता है। अतः सुविधा के लिये, सर्वप्रथम दो विमीय कार्तीय निर्देशांक तंत्र में लाप्लास समीकरण का हल ज्ञात करते हैं।
लॉप्लास समीकरण को दो कार्तीय निर्देशांक तंत्र में निम्न समीकरण से व्यक्त करते हैं।
इस समीकरण को हल करने के लिये चरों के पृथक्करण का उपयोग करते हैं जिसमें अज्ञात फलन (x,y ) को पृथक-पृथक एकल चर फलन X (x) तथा Y(y) के गुणनफल के रूप में लिखा जा सकता है अर्थात्
समीकरण (3) को समीकरण (2) में रखने पर,
X(x) Y(y) से भाग देने पर,
इस समीकरण प्रथम पद केवल एक चर x पर निर्भर करता है तथा दूसरा पद केवल अन्य चर y पर निर्भर करता है। इसका तात्पर्य हैं कि चर राशि x के परिवर्तन करने से दूसरे पद में कोई परिवर्तन नहीं होता है। इसी प्रकार चर राशि y में परिवर्तन करने से प्रथम पद में कोई परिवर्तन नहीं होता है। यह तभी सम्भव है जब दोनों पद अलग-अलग किसी नियतांक के बराबर हों। माना ये नियतांक क्रमशः k21 तथा k 22 के बराबर हैं।
समीकरण (4) से,
समीकरण (5) से,
उपरोक्त समीकरणों दो साधारण अवकल समीकरणें हैं जिनके हल निम्न होंगे।
इन हलों को समीकरण (3) में रखने पर,
जहाँ A, B, C, D नियतांक है जिनके मान समस्या के परिसीमा प्रतिबंध से ज्ञात किये जा सकते हैं। चूंकि समीकरण ( 1 ) का हल समीकरण ( 8 ) k के सभी मानों के लिये वैध रहता है अतः समीकरण (1) का व्यापक हल होगा।
k = 0 के लिये, समीकरण (6) तथा (7) के हल होंगे-
समस्या के लिये समीकरण (8), (9) व (10) में से कौन सा हल उचित होगा, यह समस्या के परिसीमा प्रतिबंध पर निर्भर करेगा ।
दो भूसम्पर्कित समांतर चालक प्लेटों के बीच रैखिक आवेश (LINE CHARGE BETWEEN TWO EARTHED PARALLEL CONDUCTING PLATES)
दो विमीय कार्तीय निर्देशांक तंत्र में लॉप्लास समीकरण के उदाहरण के रूप में, माना दो भूसम्पर्कित समांतर प्लेटों के चारों तरफ विद्युत विभव का मान ज्ञात करते हैं जब इनके बीच एक रैखिक आवेश रखते हैं। दो चालक प्लेट X-Y पल में y = 0 व y = a दूरी पर हैं जैसा कि चित्र (8.3-1) में दर्शाया गया है। दोनो चालक प्लेटों को भूसम्पर्कित किया गया है ताकि इन विभव का मान शून्य रहे। इन प्लेटों के बीच (0,d) बिंदु से पारित Z – अक्ष के समांतर एक रैखिक आवेश स्थित है। रैखिक आवेश की चौड़ाई इतनी कम है कि आवेश को डिराक डेल्टा फलन द्वारा निरूपित किया जा सकता है। माना रैखिक आवेश पर Y – अक्ष के अनुदिश वितरण निम्न फलन द्वारा दिया गया है-
जहाँ रैखिक आवेश पर आवेश प्रति एकांक लम्बाई है । ‘
रैखिक आवेश प्लेटों के मध्य क्षेत्र को दो भागों में विभाजित करते है जहाँ विभव के मान क्रमश:
है तथा इन क्षेत्रों में कोई आवेश नहीं है। प्लेटों के बीच आवेश रहित क्षेत्रों में विभव के मान ज्ञात करने के लिए दो विमीय कार्तीय निर्देशांकों वाला निम्न लॉप्लास समीकरण का उपयोग करते हैं।
इसका व्यापक हल खण्ड (8.2) के समीकरण (9) से लिख सकते हैं।
अज्ञात नियतांकों A, B, C, D तथा k का मान ज्ञात करने के लिये इस समीकरण में विभव की परिसीमा प्रतिबंध आरोपित करते है- पर,
(i) y = 0 पर विभव = 0 होता है। अतः इस प्रतिबंध को समीकरण (3) में आरोपित करने
(ii) y = a पर भी विभव | = 0 होता है।
k का मान समीकरण (4) में रखने पर,
(iv) ∞<x<0 क्षेत्र में x = ० पर विभव = 0 होता है। इस परिसीमा प्रतिबंध को 0< x < 0 क्षेत्र में आरोपित करने पर,
(v) अब A तथा Bn का मान ज्ञात करने के लिए रैखिक आवेश की परिसीमा प्रतिबंध आरोपित करते है। चूंकि आवेश की स्थिति पर विभव दोनों सतत होने चाहिए।
रैखिक आवेश की परिसीमा प्रतिबंध ( 8 ) आरोपित करने पर,
ये मान समीकरण (6) व (7) में रखने पर,
An का मान ज्ञात करने के लिए रैखिक आवेश की परिसीमा प्रतिबंध ( 9 ) को समीकरण (10) व (11) में रखने पर,
इस समीकरण के दोनो तरफ sin ( mr/a) से गुणा करके 0 व a के बीच y के सापेक्ष समाकलन करने पर,
डिराकडेल्टा फलन के निम्न गुण का उपयोग करने पर.
An का मान समीकरण ( 10 ) व ( 11 ) में रखने पर,
त्रिविमीय कार्तीय निर्देशांकों में लॉप्लास समीकरण (LAPLACE EQUATION IN THREE DIMENSIONAL CARTESIAN COORDINATES)
त्रिविमीय कार्तीय निर्देश तंत्र में लॉप्लास समीकरण है,
इस समीकरण को हल करने के लिए भी चर राशियों के पृथक्करण विधि का उपयोग करते हैं जिसमें अज्ञात फलन (x, y, z ) को तीन पृथक एकल चर फलनों X(x), Y(y) व Z(z) के गुणनफल के रूप में व्यक्त करते हैं।
समीकरण (2) को समीकरण (1) में रखने पर,
.
इसे X(x)Y(y)Z(z) से भाग देने पर,
इस समीकरण का प्रत्येक पद अलग-अलग स्वतंत्र चर राशि का फलन है। चर राशि x के परिवर्तन करने से दूसरे व तीसरे पद में कोई परिवर्तन नहीं होता है। चर राशि y में परिवर्तन करने से प्रथम व तीसरे पद में कोई परिवर्तन नहीं होता है। इसी प्रकार चर राशि 2 में परिवर्तन करने से प्रथम व दूसरे पद में कोई परिवर्तन नहीं होता है। यह तभी सम्भव है जब तीनों पद अलग-अलग किसी नियतांक के बराबर हों। माना ये स्वैच्छिक नियतांक क्रमशः -a2 – B2, तथा y2 के बराबर हैं। ये नियतांक समीकरण (3) में रखने पर,
अत: समीकरण (3) का प्रथम पद
यह एक साधारण अवकल समीकरण है अतः इसका हल निम्न होता है-
X(x) = A sin ax + B cos ax …(5a)
समीकरण (3) का द्वितीय पद
इसी प्रकार समीकरण (3) का तीसरा पद
जहाँ A, B, C, D, E, F, a व B अज्ञात राशियाँ है जिनको समस्या के परिसीमा प्रतिबंध से कर सकते हैं।
समीकरण (5) को समीकरण (2) में रखने पर त्रिविमीय लॉप्लास समीकरण का हल प्राप्त हो जाता है।
चूंकि समीकरण (1) उपरोक्त हल a व B के सभी मानों के लिये वैध है इसलिये समीकरण (1) का व्यापक हल होगा।
हिंदी माध्यम नोट्स
Class 6
Hindi social science science maths English
Class 7
Hindi social science science maths English
Class 8
Hindi social science science maths English
Class 9
Hindi social science science Maths English
Class 10
Hindi Social science science Maths English
Class 11
Hindi sociology physics physical education maths english economics geography History
chemistry business studies biology accountancy political science
Class 12
Hindi physics physical education maths english economics
chemistry business studies biology accountancy Political science History sociology
English medium Notes
Class 6
Hindi social science science maths English
Class 7
Hindi social science science maths English
Class 8
Hindi social science science maths English
Class 9
Hindi social science science Maths English
Class 10
Hindi Social science science Maths English
Class 11
Hindi physics physical education maths entrepreneurship english economics
chemistry business studies biology accountancy
Class 12
Hindi physics physical education maths entrepreneurship english economics