नियत वेग से गतिशील बिन्दुवत आवेश का विद्युत क्षेत्र ELECTRIC FIELD OF A POINT CHARGE MOVING WITH CONSTANT VELOCITY in hindi
ELECTRIC FIELD OF A POINT CHARGE MOVING WITH CONSTANT VELOCITY in hindi नियत वेग से गतिशील बिन्दुवत आवेश का विद्युत क्षेत्र क्या है ?
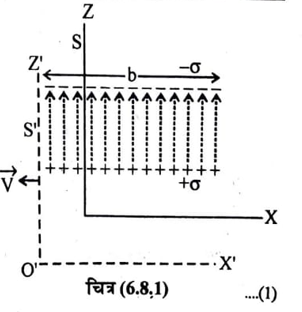
किसी अन्य जड़त्वीय निर्देश तंत्र में विद्युत क्षेत्र का मापन (ELECTRIC FIELD MEASURED IN DIFFERENT FRAMES OF REFERENCE) माना किसी स्थिर निर्देश तंत्र S ( चित्र 6.8.1 ) में समान आवेश घनत्व + तथा Coulomb/m2 से आवेशित दो वर्गाकार पट्टिकायें स्थित हैं। इन पट्टिकाओं की लम्बाई b है तथा ये X-Y तल में परस्पर समानांतर दूरी पर स्थित है। पट्टिकाओं के बीच की दूरी d उनकी लम्बाई की तुलना में बहुत कम मानी गई है ताकि पट्टिकाओं के मध्य उत्पन्न विद्युत क्षेत्र एक समान हो । जैसा कि चित्र (6.8.1) में दर्शाया है पट्टिकाओं के मध्य विद्युत क्षेत्र की तीव्रता की दिशा Z-अक्ष के अनुदिश है अतः
माना एक अन्य निर्देश तंत्र S’, स्थिर तंत्र S के सापेक्ष नियत वेग से ऋणात्मक X दिशा में गति कर रहा है। यदि जड़त्वीय निर्देश तंत्र S’ में स्थित प्रेक्षक O’ इन पट्टिकाओं को देखता है (चित्र 6.8.2 ) तो उसे पट्टिकायें वर्गाकार दिखाई नहीं देगी।
आपेक्षिकता के सिद्धान्त के अनुसार X दिशा में पट्टिकाओं की लम्बाई b से संकुचित होकर
b√1 – v2 / c2 = b/1-B2 (जहाँ 3 = v/c) हो जाती है परन्तु इनकी Y’ या Z’ दिशा में चौड़ाई में कोई परिवर्तन नहीं होता है। हम जानते हैं कि आवेश का परिमाण निर्देश तंत्र के वेग पर निर्भर नहीं करता है इसलिये निर्देश तंत्र S’ के सापेक्ष समानांतर पट्टिकाओं पर आवेश घनत्व का मान निर्देश तंत्र S की तुलना में अधिक होगा।
चूँकि निर्देश तंत्र S’ में पट्टिका का क्षेत्रफल
अतः निर्देश तंत्र S’ में पट्टिका में प्रेक्षित आवेश घनत्व होगा,
y = 1/√1-B2 है तथा सदैव 1 से अधिक होता है क्योंकि v >> c.
उपरोक्त स्थिति से यह निश्चित है कि पट्टिकाओं के बाहर विद्युत क्षेत्र शून्य होता है तथा इनके बीच में विद्युत क्षेत्र समरूपी होता है। यही शर्त अनंत विस्तार की पट्टिकाओं के लिये भी होगा। अनंत विस्तार की पट्टिकाओं के कारण विद्युत क्षेत्र पट्टिका से दूरी तथा पट्टिका पर किसी बिन्दु की स्थिति पर निर्भर नहीं करता है। अनंत विस्तार की धनावेशित तथा ऋणावेशित पट्टिकाओं के कारण विद्युत क्षेत्रों को निम्न चित्र (6.8.3) तथा चित्र (6.8.4) में दर्शाया गया है।
इन दोनों विद्युत क्षेत्रों के अध्यारोपण से उत्पन्न विद्युत क्षेत्र के प्रारूप को चित्र (6.8.5) में प्रदर्शित किया गया है।
अब माना एक स्थिर आयताकार बॉक्स के आकार का गॉसीय पृष्ठ तंत्र S’ में चित्रानुसार (6.8.5) स्थित है। गॉस के प्रमेयानुसार पट्टिकाओं के बाहर विद्युत क्षेत्र शून्य तथा पट्टिकाओं के मध्य विद्युत क्षेत्र होता
जब समांतरपट्टिकाओं की स्थिति X- अक्ष के लम्बवत हो अब पट्टिकाओं की व्यवस्था पहले की स्थिति से भिन्न लेते . हैं अर्थात् चित्रानुसार (6.8.6) पट्टिकाओं को इस प्रकार रखा गया | है कि ये निर्देश तंत्र S के X- अक्ष के लम्बवत हो। इस स्थिति में | निर्देश तंत्र S के सापेक्ष पट्टिकाओं के मध्य विद्युत क्षेत्र X- अक्ष | के अनुदिश होगा और इसका मान होता है।
यदि इन्हीं पट्टिकाओं को निर्देश तंत्र S’ के सापेक्ष देखा जाये तो पट्टिकाओं के आवेश घनत्व में कोई परिवर्तन नहीं होता है। इसका कारण है कि निर्देश तंत्र S’ के सापेक्ष पट्टिकाओं के आकार में कोई संकुचन या विस्तार नहीं होता है। (आपेक्षिकता के सिद्धान्तानुसार निर्देश तंत्र के गति के लम्बवत् दिशा में कोई परिवर्तन नहीं होता है) केवल पट्टिकाओं मध्य दूरी में कमी होती है जिसका विद्युत क्षेत्र की गणना में कही उपयोग नहीं होता है।
अब निर्देश तंत्र S’ स्थिर आयताकार बॉक्स के आकार के गॉसीय पृष्ठ की कल्पना करते हैं। चित्र (6.8.7) गॉस के प्रमेयानुसार निर्देश तंत्र S’ में पट्टिकाओं के मध्य Z विद्युत क्षेत्र की तीव्रता होगी।
विद्युत क्षेत्र के Y तथा Z घटक निर्देश तंत्र S तथा S’ के बीच की आपेक्षिक गति के दिशा के लम्बवत् होते हैं। अतः रूपांतरण पहले स्थिति के अनुसार होगा अर्थात्
उपरोक्त विश्लेषण से यह निष्कर्ष प्राप्त होता है कि यदि स्थिर आवेशों के कारण किसी स्थिर निर्देशा तंत्र S के सापेक्ष विद्युत क्षेत्र है तथा निर्देश तंत्र S के सापेक्ष X- अक्ष के अनुदिश वेग से गतिशील किसी अन्य निर्देश तंत्र S’ में उसी आवेश का विद्युत क्षेत्र हो तो E तथा E के घटकों का रूपांतरण सम्बन्ध निम्न होता है।
निर्देश तंत्र S’ की गति की दिशा के अनुदिश विद्युत क्षेत्र के घटकों के लिये
………………………..(10)
निर्देश तंत्र S’ की गति की दिशा के लम्बवत् विद्युत क्षेत्र के घटकों के लिये
नियत वेग से गतिशील बिन्दुवत आवेश का विद्युत क्षेत्र (ELECTRIC FIELD OF A POINT CHARGE MOVING WITH CONSTANT VELOCITY) माना एक स्थिर निर्देश तंत्र S के मूल बिन्दु पर विरामावस्था में कोई बिन्दुवत आवेश q स्थित है। बिन्दुव आवेश q से दूरी r पर स्थित किसी बिन्दु P(x, y) पर विद्युत क्षेत्र की तीव्रता होती है।
इसलिये बिन्दु P पर विद्युत क्षेत्र की तीव्रता के घटक होंगे चित्र (6.9.1)
यदि एक अन्य निर्देश तंत्र S’ जो प्रारम्भ t=t’ = 0 पर स्थिर निर्देश तंत्र S के साथ सम्पाती था, नियत वेग V से ऋणात्मक X- अक्ष दिशा में गतिशील है, तो निर्देश तंत्र S’ के प्रक्षेक O’ को आवेश q धनात्मक X- अक्ष की दिशा में नियत वेग V से गति करता हुआ दिखाई देगा हम निर्देश तंत्र S’ में बिन्दुवत आवेश q कारण उत्पन्न विद्युत क्षेत्र की तीव्रता का व्यंजक ज्ञात करना चाहते हैं माना स्थिर निर्देश तंत्र S में किसी घटना के निर्देशांक (x, y, z, t) है तथा गतिशील निर्देश तंत्र S”उसी घटना के निर्देशांक (x’, y’, z’, t’) है।
लॉरेंज रूपांतरण समीकरण से इन निर्देशांकों में सम्बन्ध,
…..(3)
उपरोक्त समीकरणों में ऋण चिन्ह इसलिये आता है कि हमने निर्देश तंत्र S’ के वेग को निर्देश तंत्र S के ऋणात्मक X – दिशा में माना है।
नियत वेग से गतिशील निर्देश तंत्र S’ में बिन्दुवत आवेश q के कारण P पर विद्युत क्षेत्र की तीव्रता के घटक [खण्ड (8.6) के समकरण ( 10 ) व (11) से]
‘E’x = Ex Ez = yEz
समीकरण (3) का उपयोग कर समीकरण (4) के E’x तथा Ez के मानों को निर्देश तंत्र S’ के निर्देशांकों के रूप में ज्ञात किया जा सकता है। अतः t = 0 समय पर रूपांतरण समीकरण
यदि निर्देश तंत्र S’ के सापेक्ष बिन्दु के निर्देशांक (x’, z) हों तो t = t’ = 0 पर आवेश q मूल बिन्दु O’ पर होगा
जहाँ ‘ स्थिति सदिश तथा आवेश की गति की दिशा के मध्य कोण है।
उपरोक्त मानों को समीकरण (7) में रखने पर,
….(8)
उपरोक्त समीकरण (8) से ज्ञात होता है कि गतिशील आवेश के कारण किसी बिन्दु पर विद्युत क्षेत्र की तीव्रता आवेश के गति पर निर्भर करती है । (i) आवेश की गति की दिशा में विद्युत क्षेत्र : यदि बिन्दु P गतिमान आवेश की गति की दिशा (X- अक्ष) में हो तो
(ii) आवेश की गति की दिशा के लम्बवत् विद्युत क्षेत्र : यदि बिन्दु P गतिमान आवेश की गति की दिशा के लम्बवत् दिशा (Z’-अक्ष) में स्थित हो तो
अर्थात् गतिमान आवेश के कारण किसी बिन्दु पर विद्युत क्षेत्र की तीव्रता आवेश की गति की दिशा में तीव्रता की तुलना में आवेश की गति के लम्बवत् दिशा में
(iii) यदि आवेश q का वेग v प्रकार के वेग की तुलना में बहुत कम है अर्थात् B<< 1 या y = 1, तो विद्युत क्षेत्र की तीव्रता,
यह मान निर्देश तंत्र S’ में स्थिर आवेश के कारण विद्युत क्षेत्र की तीव्रता के बराबर होता है । यदि इस प्रकार के विद्युत की तीव्रता को बल रेखाओं के द्वारा व्यक्त करें तो विद्युत क्षेत्र गोलीय सममित बल रेखाओं (spherically symmetric lines of force) के द्वारा प्रदर्शित की जा सकती है। जैसा कि चित्र (6.9.3) में दर्शाया गया है।
परन्तु यदि B का मान नगण्य नहीं है तो आवेश की गति की दिशा में विद्युत क्षेत्र की तीव्रता की तुलना में आवेश गति के लम्बवत् दिशा में तीव्रता अधिक प्रबल होती है। इस स्थिति में यदि विद्युत क्षेत्र की तीव्रता को बल रेखाओं के रूप में व्यक्त करें तो बल रेखाओं की गति के लम्बवत् दिशा में ज्यादा केन्द्रित होती हुई दिखाई देती है जैसा कि चित्र (6.9.4) में दर्शाया गया है। इस प्रकार का विद्युत क्षेत्र गोलीय सममित नहीं होता है और इसे किसी भी स्थिर आवेश वितरण द्वारा प्राप्त नहीं किया जा सकता।
हिंदी माध्यम नोट्स
Class 6
Hindi social science science maths English
Class 7
Hindi social science science maths English
Class 8
Hindi social science science maths English
Class 9
Hindi social science science Maths English
Class 10
Hindi Social science science Maths English
Class 11
Hindi sociology physics physical education maths english economics geography History
chemistry business studies biology accountancy political science
Class 12
Hindi physics physical education maths english economics
chemistry business studies biology accountancy Political science History sociology
English medium Notes
Class 6
Hindi social science science maths English
Class 7
Hindi social science science maths English
Class 8
Hindi social science science maths English
Class 9
Hindi social science science Maths English
Class 10
Hindi Social science science Maths English
Class 11
Hindi physics physical education maths entrepreneurship english economics
chemistry business studies biology accountancy
Class 12
Hindi physics physical education maths entrepreneurship english economics