gibbs phase rule in hindi formula derivation गिब्स प्रावस्था नियम की व्युत्पत्ति समीकरण समझाइये

गिब्स प्रावस्था नियम की व्युत्पत्ति समीकरण समझाइये gibbs phase rule in hindi formula derivation ?

स्वातन्त्रय कोटि (Degree of Freedom)– एक तंत्र को प्रभावित करने वाले कितने ही चरांक (Variables) होते हैं, परन्तु इनमें से ताप, दाब एवं संघटन (Composition) ही स्वतंत्र चर माने जाते हैं। किसी तंत्र की स्वातंत्रय की कोटि, “इन चराकों की वह न्यूनतम संख्या है जिन्हें, तंत्र को पूर्णतया अभिव्यक्त करने के लिये निश्चित किया जाना आवश्यक है।” स्वातंत्रय की कोटि को समझने के लिये कुछ भौतिक उदाहरण लिये जा सकते हैं। जैसे -अन्तरिक्ष (Space) में किसी गेंद की स्थिति को जानने के लिये तीन निर्देशांकों (coordinates) की मैदान में पड़ी गेंद की स्थिति जानने के लिये दो निर्देशांकों की तथा एक नाली (grove) में चलती हुई गेंद की स्थिति जानने के लिये एक निर्देशांकों की आवश्यकता होती है। इस प्रकार कहा जा सकता है कि ऊपर वर्णित तंत्रों में गेंद की स्वातन्त्रय की कोटियाँ क्रमशः तीन, दो तथा एक हैं। निम्न लिखित उदाहरणों से स्वातंत्रय की कोटि को और स्पष्ट समझा जा सकता है।

(i) KCI के जलीय विलयन की स्वातंत्रय कोटि दो होगी क्योंकि इस तंत्र को स्पष्ट करने के लिये दो चरांकों ताप व संघटन (विलयन की सान्द्रता) को निश्चित किया जाना आवश्यक है। यदि KCI का संतृप्त विलयन लिया जाता है तो इस तंत्र के बारे में जानकारी केवल एक चर ताप द्वारा की जा सकती है। क्योंकि निश्चित ताप पर संतृप्त विलयन का संघटन निश्चित होता है। अतः KCI का संतृप्त विलयन एक चर (mono varient) तथा असंतृप्त विलयन द्विचर (bivarient) होता है।

(ii) किसी पात्र में एक गैस बन्द है। इस तंत्र को अभिव्यक्त करने के लिये दो चरों (ताप व दाब) को ही निश्चित करना पड़ता है। तीसरे चर (संघटन) की आवश्यकता नहीं होती हैं क्योंकि गैस एक ही  है। जहाँ तक तंत्र में उपस्थित गैस के मोलों की संख्या का प्रश्न है, उसका मान उपर्युक्त दोनों चरों द्वारा निर्धारित किया जा सकता है। यदि तंत्र विभिन्न गैसों का मिश्रण हो तो तंत्र की अभिव्यक्ति में संघटन के रूप में तृतीय चर की भी आवश्यकता होगी। अतः तंत्र त्रिचर (Trivarient) होगा।

(iiI) किसी बन्द पात्र में यदि HO द्रव तथा H2O वाष्प से बना तंत्र है तो इस तंत्र की अभिव्यक्ति में दो (ताप व दाब) में से केवल एक चर की ही आवश्यकता होती हैं क्योकि ताप के निर्धारण करने पर वाष्प दाब स्वयं निर्धारित हो जाता है। अतः इस तंत्र की स्वातंत्रय की कोटि एक होगी।

(iv) बर्फ, जल तथा वाष्प एक बन्द बर्तन में यदि साम्यवस्था में हैं तो तंत्र की स्वातंत्रय की कोटि शून्य होगी। क्योंकि बर्फ, जल तथा वाष्प तीनों साम्यवस्था में केवल 0.0098° से. ताप. 4.58 मिमि. दाब पर ही रह सकते हैं। स्वेच्छा से हम किसी चर को निर्धारित नहीं कर सकते। इस अवस्था में यह तंत्र अचर (Non-varient) तंत्र कहलाता है।

यहाँ यह बात समझ लेना आवश्यक है कि एक बीकर में सामान्य ताप एवं एक वायुमण्डल पर बर्फ, जल व वाष्प तीनों प्रावस्थायें उपस्थित रह सकती हैं, परन्तु साम्यवस्था में नही होती है कुछ समय बाद बर्फ गल जाती हैं।

प्रावस्था नियम के लाभ (Advantages of Phase Rule)

जैसा कि प्रारम्भ में बताया गया है, प्रावस्था नियम ऊष्मागतिकी पर आधारित है जो कि एक यथार्थ विज्ञान (exact science) है। अतः प्रावस्था नियम को एक यथार्थ नियम कहा जा सकता है। इस नियम द्वारा विषमांगी साम्य के अध्ययन में कुछ लाभ हैं, जिन्हें निम्न प्रकार वर्णित किया जा सकता है-

(i) भौतिक (Physical ) तथा रासायनिक (chemical) दोनों प्रकार के विषमांगी साम्यों का अध्ययन इस नियम द्वारा किया जा सकता है।

(iI) पदार्थ की मात्रा, प्रकृति अथवा अभिक्रिया का प्रावस्था नियम से कोई संबंध नहीं, मात्र प्रावस्था संख्या तथा उनका संघटन ही तंत्र के अध्ययन के लिये पर्याप्त है।

(iiI) प्रावस्था नियम प्रयोग करते समय पदार्थ की संरचना (constitution) के बारे में किसी पूर्वधारणा की आवश्यकता नहीं है।

(iv) भिन्न-भिन्न प्रकार के विषमांगी साम्यों को स्वातन्त्रय की कोटि के आधार पर एक साथ वर्गीकृत करने की आवश्यकता नहीं है।

(v) प्रावस्था नियम, विभिन्न तंत्रों के आचरण के पूर्वानुमान में सहायक है।

 प्रावस्था नियम की सीमायें ( Limitations of Phase Rule)

प्रावस्था नियम का उपयोग करते समय निम्नलिखित सीमाओं का ध्यान रखना आवश्यक है।

(i) प्रावस्था नियम में केवल ताप, दाब व संघटन अर्थात् तीन चरों पर ही विचार किया गया हैं जबकि चुम्बकीय, विद्युत एव विकिरणशील प्रभावों जैसे चरों पर विचार नहीं किया गया है।

(ii) प्रावस्था नियम में गुरूत्वाकर्षण बल पर भी विचार नहीं किया गया है।

(iiI) कोई प्रावस्था ठोस अथवा द्रव इतनी सूक्ष्म विभाजित (finely divided) नहीं होनी चाहिये कि वह पृष्ठ तनाव तथा वाष्प दाब से प्रभावित हो जाये।

(iv) कुछ विशेष अवस्थाओं में प्रावस्था नियम पर कुछ अतिरिक्त मर्यादायें लगानी पड़ती हैं, ऐसी अवस्था में मर्यादित प्रावस्था नियम (Phase rule under restricted condition or restricted phase rule) का उपयोग करते हैं।

गिब्स प्रावस्था नियम की व्युत्पत्ति (Derivation of Gibbs Phase Rule)

माना कि साम्यावस्था में स्थित किसी विषमांगी तंत्र में P प्रावस्थाएं तथा C घटक है तंत्र की स्वतंत्रता की कोटि या चरों की संख्या F है। यह संख्या उस संख्या के बराबर होगी जिन्हें तंत्र को पूर्णत: करने के लिए स्वेच्छतः निश्चित कर दिया जाता है। चूंकि तंत्र की अवस्था ताप व दाब पर निर्भर होगी अतः तंत्र में दो चर तो होगे ही। सान्द्रता चर प्रावस्थाओं की संख्या पर निर्भर होते हैं। यदि किसी प्रावस्था में C घटक हो तो एक घटक को छोड़कर अन्य घटकों की सान्द्रता का संघटन ज्ञात हो तो उसे एक घटक की सान्द्रता बची हुई सान्द्रता से ज्ञात की जा सकती है। अतः एक घटक वाली प्रावस्थाओं (C-1) चरों (सान्द्रता पदों) की सान्द्रता निश्चित करना आवश्यक है। उस आधार पर P प्रावस्था वाले तंत्र में सान्द्रता चरों की कुल संख्या P (C-1) की आवश्यकता होगी। ताप तथा दाब चरों को सम्मिलित करने

पर चरों की कुल संख्या = P (C – 1 ) + 2 होगी।

ऊष्मागतिकी के अनुसार जब कोई विषमांगी तंत्र स्थिर ताप व दाब पर साम्य में होगा तो किसी दिए हुए घटक का रासायनिक विभव (u) प्रत्येक प्रावस्था में समान होगा। माना कि एक घटक (i) तीन प्रावस्थाओं a, b और c में है। तो घटक (i) को इन दो समीकरणों के रूप में लिखा जा सकता है-

अतः प्रत्येक घटक जिसके तीन प्रावस्थायें साम्य में हों उपरोक्त दो समीकरण ज्ञात होते हैं। इसलिये सामान्यतया प्रत्येक घटक के P प्रावस्थाओं में होने पर (P- 1) समीकरण ज्ञात होगे। इसलिये C घटकों के लिए C (P – 1) समीकरण ज्ञात होगें। चूंकि रासायनिक विभव दाब, ताप तथा संघटन का फलन होता है। इसका तात्पर्य यह है कि प्रत्येक समीकरण एक चर को प्रदर्शित करता है।

अतः कुल ज्ञात चरों की संख्या = C (P-1 )

चूंकि कुल चरों की संख्या = P (C-1) + 2

अतः अज्ञात चरों की संख्या कुल चरों की संख्या कुल ज्ञात चरों की संख्या

= P (C-1) + 2 – C (P- 1)

= PC – P + 2 – CP + C

=C – P + 2

अर्थात् तंत्र को पूर्णतया परिभाषित करने के लिये इन चरों की संख्या को स्वेच्छा से निश्चित कर देते हैं। इसलिये ये तंत्र की स्वतंत्रता की कोटियों की संख्या के बराबर होगी अर्थात्

F = C – P + 2

F + P = C + 2

यही प्रावस्था नियम है जिसको गिब्स ने 1876 में प्रतिपादित किया था अतः इसे गिब्स का प्रावस्था नियम कहते हैं।

 प्रावस्था नियम के अनु (Application of Phase rule )

 एक घटक तंत्र (One Component System)

जल तंत्र, गंधक तंत्र, कार्बन डाइऑक्साइड तंत्र, फॉस्फोरस तंत्र आदि एक घटक तंत्रों की श्रेणी में आते हैं। यहाँ केवल प्रथम तीन तन्त्रों को ही समझाया गया है।

एक घटक तंत्र में C= 1 है C का यह मान प्रावस्था नियम में रखने पर

F – 1 – P + 2

F = 3 – P

किसी भी तंत्र में प्रावस्था की न्यूनतम संख्या । हो सकती है अर्थात् P = 1 | अतः स्वातंत्र्य की कोटि (F) का अधिकतम मान 2 होगा। अर्थात् तंत्र की पूर्ण अभिव्यक्ति के लिये अधिकतम 2 चरों की आवश्यकता होगी जो कि क्रमशः ताप तथा दाब है। चूंकि किसी एक घटक तंत्र में प्रावस्था का संघटन बदलता नहीं है, अत यह चर नहीं है ।

चूंकि स्वातंत्र्य की कोटि का न्यूनतम मान शून्य हो सकता है अतः उपर्युक्त समीकरण के अनुसार प्रावस्था का अधिकतममान 3 हो सकता है।

उपर्युक्त कथनों से दो महत्वपूर्ण निष्कर्ष निकाले जा सकते हैं-

(i) एक घटक तंत्रों को दो चरों द्वारा व्यक्त किया जा सकता है। अर्थात् प्रावस्था आरेख (Phase diagram) को दो अक्षों ताप व दाब द्वारा समझाया जा सकता है। इस आरेख को ताप-दाब आरेख (Temperatur -Pressure diagram) कहते हैं।

(ii) एक घटक तंत्रों में अधिक से अधिक तीन प्रावस्थाएँ साम्यावस्था में रह सकती है। 4.7.2 जलतन्त्र (Water System)

जल तंत्र एक घटक तंत्र है इसकी तीनों प्रावस्थाऐं इस प्रकार है।

जल तंत्र का प्रावस्था आरेख प्राप्त करने के लिये एक बन्द पात्र में जल एवं वाष्प लिया जाता है।

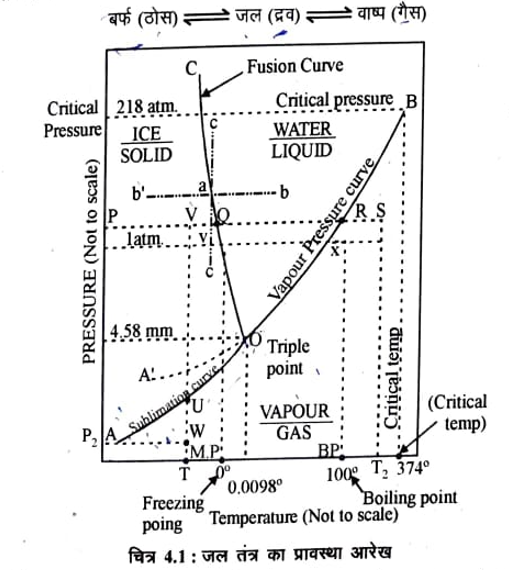
अब इस पात्र के ताप में परिवर्तन किया जाता है और तंत्र के वाष्प दाब को मापा जाता है। ताप व दाब के इन मानों से भिन्न भिन्न वक्र प्राप्त होते हैं। चित्र (4.1) में जल तंत्र का प्रावस्था आरेख दर्शाया है। जिसमें प्राप्त वक्रों, वक्रों के प्रतिच्छेदन बिन्दु (Point of intersection) एवं वक्रों से घिरे क्षेत्रों को दर्शाया गया है।

जल तंत्र के मुख्य लक्षण निम्नलिखित है।

(i) वक्र OA OB तथा OC एक चर तंत्र को प्रदर्शित करते हैं।

(ii) इन वकों से घिरे तीन क्षेत्र द्विवर तंत्र को प्रदर्शित करते हैं।

(a) ये तीनों व बिन्दू 0 पर मिलते हैं जो कि एक त्रिक बिन्दु है तथा अपर तंत्र को प्रदर्शित करता है।

अब हम इन वनों क्षेत्रों तथा त्रिक बिन्दु की सार्थकता (significance) का अध्ययन करेंगे।

(i) वक्र (Curves)-

(a) वक्र OA यह वक्र ठोस वाष्प साम्य प्रदर्शित करता है। अतः इसे ऊर्ध्वपातन वक्र (Sublimation Curve) कहा जाता है। इस वक्र पर निम्न साम्य स्थापित रहता है।

बर्फ  => वाष्प

इस वक्र पर दो प्रावस्थाएँ विद्यमान हैं (P=2) चूंकि तंत्र में घटकों की संख्या एक है, (C = 1) अत: ये मान प्रावस्था में रखने पर

F =1 – 2 + 2 = 1

अर्थात् वक्र पर तंत्र की स्वातंत्र्य कोटि की संख्या 1 है। इस प्रकार तंत्र को व्यक्त करने के लिये केवल एक चर ताप या दाब की ही आवश्यकता होती है। दूसरा चर स्वतः निश्चित हो जाता है। वक्र से यह भी स्पष्ट है कि दाब के प्रत्येक मान के लिए ताप का एक ही मान संभव होगा। वक्र के नीचे का सिरा A परम ताप तक जाता है, जिसके नीचे ताप कम करना संभव नहीं होता है।

(b) वक्र OB- यह वक्र द्रव वाष्प साम्य प्रदर्शित करता है। अतः इसे जल का वाष्प दाब वक्र (Vapour pressure Curve) कहा जाता है। इस वक्र पर निम्न साम्य स्थापित रहता है।

जल => वाष्प

अतः इस वक्र पर प्रत्येक बिन्दु पर दो प्रावस्थाएँ (P=2) उपस्थित है चूंकि C= 1 है अतः F = 1 होगा। अर्थात् इस वक्र पर भी तंत्र एक चर होगा। वक्र पर बिन्दु X जल का क्वथनांक Tb (B.P= 100°C) बताता है, क्योंकि इस ताप पर जल का वाष्प दाब एक वायुमण्डल दाब के बराबर है। जैसे-जैसे तंत्र का ताप बढ़ाया जाता है। वाष्प दाब बढ़ता जाता है। क्रान्तिक ताप Tc (374°C) पर जल और वाष्प का घनत्व समान हो जाता है और जल उपस्थित नहीं रहता । चित्र में यह बिन्दु B द्वारा प्रदर्शित किया गया है। क्रान्तिक घटना एक निश्चित ताप (374° से.) तथा निश्चित दाब 218 वायुमण्डल (क्रान्तिक दाब) पर होती है।

(c) वक्र OC- यह वक्र ठोस द्रव साम्य प्रदर्शित करता है। अतः इसे बर्फ का गलन वक्र (Fusion Curve) कहते हैं। इस वक्र पर निम्न साम्य स्थापित रहता है।

बर्फ = > जल

इस वक्र पर प्रत्येक बिन्दु पर दो प्रावस्थाएँ उपस्थित रहती हैं (P= 2) चूंकि C = 1 है अतः F =1

अर्थात इस वक्र पर तंत्र एक चर होगा। वक्र पर बिन्दु Y बर्फ का गलनांक (MP = 0°C) बताता है। बर्फ के गलन वक्र का झुकाव (inclination) यह प्रदर्शित करता है कि दाब बढ़ाने पर बर्फ का गलनांक कम होता है।

(d) वक्र 0A’ – इसे अतिशीतलन (Supercooling) वक्र कहते हैं। यहाँ जल और वाष्प दो प्रावस्थाएँ हैं परन्तु जल मितस्थायी (metastable) अवस्था में हैं।

(ii) वक्रों से घिरे क्षेत्र (Areas enclosed by curves )-

विभिन्न वक्रों द्वारा सम्पूर्ण क्षेत्र तीन भागों में बंट जाता है।

(a) वक्र OA, OC तथा दाब अक्ष से घिरा क्षेत्र (क्षेत्र AOC)- इस क्षेत्र में केवल एक प्रावस्था बर्फ (ठोस) है। अत: P = 1. C = 1 है। यह मान प्रावस्था नियम में रखने पर

F = 1 – 1 + 2

F = 2

स्वातन्त्र्य कोटि का मान दो प्राप्त होता है। अतः इस क्षेत्र में तंत्र को पूर्णतया अभिव्यक्त करने के लिये ताप तथा दाब दोनों को निश्चित करना आवश्यक है। चित्र से यह बात भी स्पष्ट है कि इस क्षेत्र में किसी बिन्दु को व्यक्त करने के लिये दो निर्देशांकों की आवश्यकता होगी। इस प्रकार इस क्षेत्र में तंत्र द्विचर होगा।

(b) वक्र OA, OB तथा दाब अक्ष से घिरा क्षेत्र (क्षेत्र AOB)- इस क्षेत्र में भी केवल एक प्रावस्था वाष्प (गैस) है। चूंकि घटकों की सख्या भी केवल एक है, अतः प्रावस्था नियम के अनुसार इस क्षेत्र में तंत्र की स्वातंत्र्य की कोटि दो है और तंत्र द्विचर है।

(c) वक्र OC तथा OB से घिरा क्षेत्र (क्षेत्र BOC)- इस क्षेत्र में केवल प्रावस्था जल (द्रव) है। अतः इस क्षेत्र में तंत्र को पूर्ण अभिव्यक्त करने के लिये ताप व दाब दोनों की ही आवश्यकता होती है ।

क्षेत्रों की सार्थकता (Significance of Areas) – क्षेत्रों की सार्थकता समझने के लिये एक बिन्दु “a” वक्र OC पर लेते हैं। इस बिन्दु पर बर्फ तथा जल दो प्रावस्था साम्यावस्था में है। यदि स्थिर दाब पर ताप बढ़ाया जाता है तो उपस्थित बर्फ पिघल कर जल में परिवर्तित हो जाता है। चित्र में यह परिवर्तन बिन्दुकित रेखा (dotted line)ab द्वारा दिखाया गया है। इसी प्रकार स्थिर दाब पर ताप कम किया जाता है तो जल का बर्फ में परिवर्तन हो जायेगा जो कि रेखा ab’ द्वारा दिखाया गया है।

यदि स्थिर ताप पर दाब बढ़ाया जाता है तो बर्फ जल में बदल जाती है और यदि दाब कम किया जाता है तो जल बर्फ में बदल जाता है, को क्रमशः ac तथा ac’ बिन्दुकित रेखाओं द्वारा दिखाया गया है।

इसी प्रकार के बिन्दु वक्र OA तथा OB पर लिये जा सकते हैं और क्षेत्रों की सार्थकता समझाई जा सकती है।

(ii) त्रिक बिन्दु “O” (Triple Point)-

प्रावस्था आरेख में O एक ऐसा बिन्दु है, जहाँ तीनों वक्र मिलते हैं। इस बिन्दु को त्रिक बिन्दु कहते हैं। इस बिन्दु पर तीन प्रावस्थाएँ बर्फ, जल व वाष्प साम्यवस्था में है, यह साम्य इस प्रकार प्रदर्शित किया जा सकता है।

चूंकि P = 3 तथा C = 1 है। ये मान प्रावस्था नियम में रखने पर

अतः इस बिन्दु पर तंत्र की स्वातन्त्र्य कोटि शून्य है। अर्थात् तंत्र अचर है। इस बिन्दु पर तंत्र को पूर्ण रूप से व्यक्त करने के लिये ताप व दाब किसी के निर्धारण की आवश्यकता नहीं होती उनके मान  स्वयं निर्धारित है, जो कि क्रमशः 0.0098°C तथा 4.58 मिमी. है। दूसरे शब्दों में कहा जा सकता है किये तीनों प्रावस्थाऐं केवल एक ताप 0.00098°C तथा एक दाब 4.58 मिमी. पर ही साम्यावस्था में रह सकती हैं। इनमें से किसी एक का परिवर्तन करने मात्र से ही एक या दो प्रावस्थायें समाप्त हो जाती। है।

मितस्थायी साम्य (Metastable Equilibrium)-जब जल को ठण्डा किया जाता है तो उसके वाघ दाब में कमी आ जाती है, और वक्र BO प्राप्त होता है। वक्र पर बिन्दु 0 पर जल का बर्फ में परिवर्तन प्रारम्भ हो जोना चाहिये, परन्तु कभी-कभी ताप जमाव बिन्दु से नीचे हो जाने पर भी बर्फ बनना प्रारम्भ नहीं होता और जल द्रव ही बना रहता है। यह जल का अतिशीतलन (super cooling) कहलाता है। इस प्रकार वक्र OA’ प्राप्त होता है जो कि वक्र BO का ही विस्तार (extension) है। वक्र OA’ पर जल और वाष्प दो प्रावस्थायें ही हैं, परन्तु जल मितस्थायी (metastable) अवस्था में है। जैसे ही बर्फ का एक छोटा टुकड़ा इस साम्य में डाला जाता है तो सम्पूर्ण जल, बर्फ में परिवर्तित हो जाता है। OA’ वक्र का OA के ऊपर होना इस बात को प्रदर्शित करता है कि एक निश्चित ताप पर मितस्थायी साम्य का वाष्प दाब, स्थायी के वाष्प दाब से अधिक होता है।

दाब अथवा ताप में परिवर्तन करने पर होने वाले परिवर्तन (Effect of change in Temperature & Prssure on the system)- तंत्र के दाब या ताप में परिवर्तन को प्रावस्था नियम के अनुसार द्वारा आरेख की सहायता से समझाया जा सकता है माना कि प्रावस्था आरेख 4.1 में स्थिर दाब P पर बिन्दु P से S तक गर्म करने पर तंत्र में क्या परिवर्तन होगें। या स्थिर दाब P पर तथा किसी निश्चित ताप T जो चित्र में V बिन्दु द्वारा दिखाया है गर्म करने पर बर्फ पर क्या प्रभाव पड़ेगा ? चूंकि यह तंत्र द्विचर है अतः समान दाब P पर ताप का मान कुछ भी हो सकता है अतः स्थिर दाब P पर बर्फ को धीरे-धीरे गर्म करने पर तंत्र रेखा PQ पर Q की ओर विस्थापित होगा बिन्दु V से Q तक बर्फ स्थायी अवस्था में रहेगा व बिन्दु Q पर पिघलने लगेगी तथा द्रव प्रावस्था प्राप्त होगी। जब तक बर्फ पूर्ण रूप से नही पिघल जाती है तब तक ताप स्थिर रहेगा। इसके बाद तंत्र ताप रेखा QR पर R की ओर बढ़ना चालू हो जाएगा। और जब तक जल का पूरी तरह वाष्प में परिवर्तन न हो जाए ताप स्थिर ही रहेगा। जब जल प्रावस्था पूर्णतया अदृश्य हो जाती है तो तंत्र में केवल एक प्रावस्था वाष्प होती है व तंत्र पुनः द्विचर हो जाता है आगे फिर ताप बढ़ाने पर वाप का ताप रेखा RS के सहारे बढ़ता है व बिन्दु s पर T2 हो जाता है।

इसी प्रकार T बिन्दु पर ताप T स्थिर हुए बिन्दु V पर दाब कम करने पर तंत्र रेखा VU के सहारे बिन्दु U पर पहुँचेगी। बिन्दु V से U तक बर्फ स्थायी अवस्था में रहेगी (द्विचर) बिन्दु U पर बर्फ ऊर्ध्वपातित होना प्रारम्भ हो जावेगी और वाष्प में परिवर्तित हो जावेगी (एकचर)। जब ठोस प्रावस्था पूर्णतया अदृश्य हो जाती है तो तंत्र में एक प्रावस्था वाष्प होती है व तंत्र पुनः द्विचर हो जाता है। आगे दाब और कम करने पर रेखा UW के सहारे चलती है। वाष्प का दाब U बिन्दु पर P2 हो जायेगा |

इस प्रकार ताप व दाब दोनों में परिवर्तन होने पर तंत्र के व्यवहार का पता लगाया जा सकता है।

जल तंत्र की प्रमुख विशेषताओं को संक्षेप में सारणी 4.1 में दर्शाया गया है।