third law of thermodynamics in hindi ऊष्मागतिकी का तृतीय नियम क्या है समझाइए
ऊष्मागतिकी का तृतीय नियम क्या है समझाइए
एन्ट्रोपी तथा ऊष्मागतिकी प्रायिकता (Entropy and Thermodynamic Probability) एक तंत्र निश्चित ऊष्मागतिक अवस्था में जितने प्रकार से रह सकता है वह उस तंत्र की ऊष्मागतिक प्रायिकता कहलाती है। इसे सामान्यतया W से प्रदर्शित करते हैं। ऊष्मागतिक प्रायिकता को एक भौतिक उदाहरण द्वारा समझाया जा सकता है । लकडी का एक बाक्स है जो दो भागों में बंटा हुआ है। प्रत्येक भाग में दो गेंद रखी जा सकती है। चित्र 2.6 में गेंद रखने का स्थान दिखाया गया है।
माना कि एक बॉक्स मे दो गेंदे रखनी है, इन गेदों को रखने के चित्र 2.7 में दिखाये अनुसार 6 विभिन्न प्रकार हो सकते हैं। चित्र में गेंद के स्थान को • से तथा खाली स्थान को द्वारा दिखाया गया है ।
उपरोक्त स्थितियों में से गेंदों की 4 स्थितियों में एकरूपता है। अर्थात् बॉक्स के प्रत्येक भाग में एक-एक गेंद भरी हुई है। अतः गेंदों की स्थितियों में एकरूपता की प्रायिकता 4/6 एकहैं, जबकि बॉक्स के ही भाग में दोनों गेंदों के पाये जाने की प्रायिकता 2/6केवल है।
उपरोक्त कथन से स्पष्ट है कि बॉक्स के प्रत्येक भाग में एक गेंद के पायें जाने की प्रायिकता उच्चतम है।
हमें ज्ञात है कि एन्ट्रोपी तंत्र में अव्यवस्था (Disorder) का माप है। अधिकतम अव्यवस्था तब प्राप्त होती है जबकि अणु अधिकतम सम्भव स्थितियों में वितरित हो, अर्थात ऊष्मागतिक प्रायिकता उच्चतम हो। चूंकि किसी प्रक्रम में एन्ट्रोपी तथा ऊष्मागतिक प्रायिकता साथ-साथ बढ़ती है अतः साम्यवस्था को अधिकतम प्रायिकता की स्थिति माना जा सकता है। इस प्रकार यदि किसी प्रक्रम को स्वतंत्र छोड़ दिया जाये तो वह साम्यावस्था की ओर अग्रसर होता है। चूंकि सभी स्वतः प्रक्रमों में एन्ट्रोपी बढ़ती है, अतः यह कहा जा सकता है कि सभी स्वतः प्रक्रम कम प्राययिक अवस्था (Less probable state) से अधिक प्राययिक अवस्था (More probable state) की ओर बढ़ते हैं।
इस तर्क के आधार पर यह कहा जा सकता है कि एन्ट्रोपी (S) तथा ऊष्मागतिक प्रायिकता (W) सीधा सम्बन्ध है अथवा एन्ट्रोपी ऊष्मागतिक प्रायिकता का फलन है।
S = f(W) ……………………….(119)
माना कि दो तंत्र, जिनकी एन्ट्रोपी क्रमशः S1 तथा S2 है तथा ऊष्मागतिक प्रायिकता W1तथा W2 है। चूंकि एन्ट्रोपी एक योगशील गुण (additive property ) है अतः संयुक्त तंत्र की एन्ट्रोपी S का मान निम्न प्रकार से लिखा जा सकता है।
S = S1 + S2 = f(W1) + f (W2)…………….(120)
प्रायिकता एक गुणात्मक कारक (Multiple factor ) है अतः संयुक्त तंत्र की परिणामी प्रायिकता (W) को निम्न प्रकार से लिखा जा सकता है।
W = W1 × W2 ………………………..(121)
समीकरण (120) व (121) से S या W का मान समीकरण ( 119 ) में रखने पर –
f(W1) + f(W2) = f(W1 × W2)…………..(122)
उपरोक्त समीकरण तब ही सही हो सकती है जबकि फलन लघुगणकीय (Lograthamic) हो-
अतः S = k InW + C ……….(123)
यहाँ k तथा C नियतांक है। यह पाया गया है कि k वोल्ट्जमान स्थिरांक है एम. प्लांक (M. Plank) ने सन् 1912 में C का मान शून्य प्रस्तावित किया । अतः समीकरण (123) निम्न प्रकार लिखी जा सकती
है।
S = kIn W……………(124)
यह समीकरण वोल्ट्ज़मान प्लांक समीकरण (Boltzman Plank Equation) कहलाती है।
परम शून्य ताप (Absolute zero) पर पूर्णतया क्रिस्टलीय पदार्थ में केवल एक ही व्यवस्था संभव है। अतः समीकरण (86) से स्पष्ट है कि इस ताप पर पदार्थ की एन्ट्रोपी शून्य होगी (ऊष्मागतिकी का तृतीय नियम)
ऊष्मागतिकी का तृतीय नियम (The Third Law of Thermodynamics)
स्थिर दाब पर किसी पदार्थ की एन्ट्रोपी में ताप के साथ परिवर्तन को निम्न समीकरण द्वारा दर्शाया जाता है।
माना कि एक ठोस को OK से TK तक स्थिर दाब पर गर्म किया जाता है ताप T ठोस के गलनांक
से कम है।
ठोस (OK,P) ठोस (TK. P)
इस प्रक्रम में होने वाले एन्ट्रोपी परिवर्तन को ज्ञात करने के लिये उपरोक्त समीकरण को ताप की 0 तथा T सीमा में समाकलित करने पर
यहाँ S0 एन्ट्रोपी का शून्य परमताप पर मान है जो कि एक काल्पनिक राशि (Hypothetical value)
है। चूंकि Cp/T का मान हमेशा धनात्मक होता है अतः उच्च ताप पर एन्ट्रोपी का मान S0 मान से
अधिक होगा। एम. प्लांक (M.Plank) ने सन् 1913 में बताया कि शुद्ध पूर्णतया क्रिस्टलीय ठोसों के S का मान शून्य होता है। यह प्रेक्षण ऊष्मागतिकी का तृतीय नियम कहलाता है। इसके अनुसार, शुद्ध एवं पूर्णतया क्रिस्टलीय ठोसों की एन्ट्रोपी का मान शून्य परमताप पर शून्य होता है। इसे गणितीय रूप में इस प्रकार लिखा जा सकता है-
समीकरण (125) में ऊष्मागतिकी का तृतीय नियम लगाने पर
Sr जो कि ठोस की परम निरपेक्ष एन्ट्रोपी (absolute entropy) कहलाती है, जो हमेशा धनात्मक
यहाँ Sr तृतीय नियम एन्ट्रोपी (Third Law Entropy) कहलाती है। तृतीय नियम प्रथम एवं द्वितीय नियम के समान किसी नई अवधारणा (Concept) को जन्म नहीं देता बल्कि यह एन्ट्रोपी के मान की सीमा निर्धारित करता है।
नर्स्ट का ऊष्मा सिद्धान्त (Nernst Heat Theorem)
जूल थामसन ने डेनीयल सैल के लिए G व H दोनों पदों का मान समान बताया। इसी प्रकार बर्थलोट के अनुसार जब अभिक्रिया से ऊष्मा निकलती है तो तन्त्र की मुक्त ऊर्जा में कमी होती है तथा इन्होने G व H में मात्रात्मक सम्बन्ध बताया जो साधारण ताप पर संघनित तन्त्र के लिए सही है। गिब्ज हेल्मोट्ज ने स्थिर दाब पर G व H में मात्रात्मक सम्बन्ध व्युत्पित किया जो इस प्रकार है—
इसे गिब्ज हेल्मोल्ट्ज समीकरण के नाम से जानते हैं। लेकिन कुछ सीमाऐं है- 1902 में रीचर्डसन ने विभिन्न तापों पर सैल के विद्युत वाहक बल ज्ञात करने पर पाया कि निश्चित दाब पर का मान ताप घटने के साथ-साथ धीरे-धीरे (Gradually) घटता जाता है। फलस्वरूप जैसे ताप घटता जाता है वैसे ही G का मान H के मान के सन्निकट (Approaches) होता जाता है। अंततः परमशून्य ताप (T = 0 ) पर
इसका तात्पर्य यह हुआ कि परम शून्य ताप (Absolute zero) पर G व H समान होते हैं।
1906 में नर्स्ट ने प्रायोगिक रूप से बताया कि का मान तापक्रम कम होने पर कम होता है।
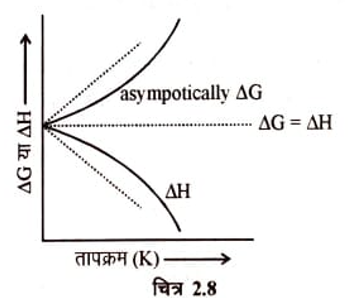
उसके अनुसार किसी संघनन तंत्र के ताप को क्रमशः परम शून्य (OK) तक कम करने पर का मान क्रमागत या उपगामी रूप से (Asympotically) घटते हुए शून्य की ओर अग्रसर होता है” इसे ही नर्स्ट का ऊष्मा सिद्धान्त कहते हैं।
इस सिद्धान्त के अनुसार परम शून्य ताप पर न केवल G तथा H के मान परस्पर समान हो जाते हैं बल्कि परमशून्य के निकट के तापों पर वे शनेः शनेः एक दूसरे की ओर अग्रसर होते हैं चित्र 2.8 में यह आचरण ठोस रेखाओं द्वारा प्रदर्शित किया गया है न कि अपुर्ण रेखाओं द्वारा जो कि परमशून्य पर शनैः शनेः न होकर तीव्र गति से आकर मिलती है।
नर्स्ट के सिद्धान्त का गणितीय रूप इस प्रकार है
नर्स्ट ऊष्मा सिद्धान्त का निष्कर्ष (Consequences of Nernst Heat Theorem)
(i) हम जानते हैं कि
दूसरे शब्दों में परम शून्य के क्षेत्र में (Vicinity of absolute zero) सारे प्रक्रम बिना एन्ट्रोपी परिवर्तन के होते हैं। यह नर्स्ट ऊष्मा सिद्धान्त का दूसरा कथन है।
(i) हम जानते हैं कि Cp व H में परिवर्तन को निम्न प्रकार व्यक्त करते हैं।
समीकरण (133) निश्चित दाब पर तंत्र की ऊष्मा धारिता का अन्तर (Cp) परमशून्य की तरफ बढ़ने पर भी शून्य की ओर बढ़ता है अर्थात् परम शून्य के आस-पास ऊष्मा धारिता अपरिवर्तित रहती है। यह भी नर्स्ट ऊष्मा सिद्धान्त का महत्वूपर्ण निष्कर्ष है ।
हिंदी माध्यम नोट्स
Class 6
Hindi social science science maths English
Class 7
Hindi social science science maths English
Class 8
Hindi social science science maths English
Class 9
Hindi social science science Maths English
Class 10
Hindi Social science science Maths English
Class 11
Hindi sociology physics physical education maths english economics geography History
chemistry business studies biology accountancy political science
Class 12
Hindi physics physical education maths english economics
chemistry business studies biology accountancy Political science History sociology
English medium Notes
Class 6
Hindi social science science maths English
Class 7
Hindi social science science maths English
Class 8
Hindi social science science maths English
Class 9
Hindi social science science Maths English
Class 10
Hindi Social science science Maths English
Class 11
Hindi physics physical education maths entrepreneurship english economics
chemistry business studies biology accountancy
Class 12
Hindi physics physical education maths entrepreneurship english economics