आण्विक वेग किसे कहते हैं molecular velocity of gases in hindi | आण्विक वेगों का मैक्सवेल वितरण (MAXWELL’S DISTRIBUTION OF MOLECULAR VELOCITIES)
इसमें जान पाएंगे कि आण्विक वेग किसे कहते हैं molecular velocity of gases in hindi | आण्विक वेगों का मैक्सवेल वितरण (MAXWELL’S DISTRIBUTION OF MOLECULAR VELOCITIES) ?
आण्विक वेग (MOLECULAR VELOCITIES)
गैसों के अणुगति सिद्धान्त के अनुसार गैसों के अणु सदैव गतिमान रहते हैं और वे सदैव सीधी रेखा में गति करते हैं, किन्तु गति करते समय वे परस्पर एक-दूसरे के साथ एवं पात्र की दीवारों के साथ टकराते रहते हैं। टक्करों के कारण इन अणुओं की गति की दिशा तथा इनकी गतिज ऊर्जा में परिवर्तन आ जाता है। और ऐसा होने से उनकी गति अथवा वेग में भी परिवर्तन आ जाएगा। अतः समस्त अणु भिन्न-भिन्न ऊर्जा वाले होते हैं और भिन्न-भिन्न गति से वे चलते हैं और इनके आण्विक वेगों को कई प्रकार से परिभाषित करते हैं।
- वर्ग माध्य मूल वेग (Root mean square velocity) – यदि किसी गैस के समस्त अणुओं के वेगों के वर्ग के औसत का वर्गमूल ज्ञात किया जाए तो उसे वर्ग माध्य मूल वेग कहते हैं। संक्षिप्त में हम इसे rms वेग कहते हैं। इसको c द्वारा प्रदर्शित करते हैं अतः ।
C = (c21 + c22 + c23 + ………+ c2n/N)1/2
जहां C1, C2, C3, …, आदि N अणुओं के व्यक्तिगत वेग हैं। इसे निम्न प्रकार भी लिखा जा सकता है
C = (nic21 + n2c22 + n3c23 + …..+ nic2i/n1 + n2 + n3 + ……+ni)1/2
= (Σnici2/ Σni2)1/2
जहा 11 अणु 61 वेग वाले, n2 अणु c2 वेग वाले, n3 अणु c3 वेग वाले,……….तथा ni अणु ci वेग वाले हैं।
इसका परिकलन गैसों की अणुगति समीकरण के आधार पर किया जाता है। PV = 1/3 mnc2
आण्विक वेगों का मैक्सवेल वितरण (MAXWELL’S DISTRIBUTION OF MOLECULAR VELOCITIES)
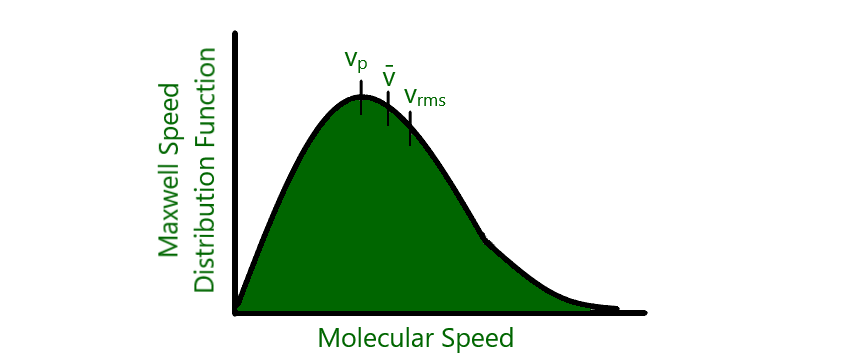
अणुओं के मध्य वेगों के वितरण को सर्वप्रथम जे सी मैक्सवेल (James Clark Maxwel) ने सर 1865 में लक्ष्य करके उनकी गणना की और आण्विक वेगों का वितरण नियम दिया जिसक अनसार आ. का गमन (motion) सर्वथा अनिश्चित रहता है. वे किसी भी दिशा में, शून्य से अनन्त तक किसी भी से गमन कर सकते है। इनके गमन की सम्भावना (nrobability) समस्त दिशाआ म समान होती है. अब इनका औसत वेग (average velocity) जो कि एक सदिश राशि (vector quantity) है, शून्य होता है। लेकिन इनकी औसत गति (average speed) जो कि एक अदिश राशि (scalar quantity) है, शून्य से अनन्त तक किसी भी मान की हो सकती है। मैक्सवेल ने गणितीय उपचार के बाद जो अन्तिम समीकरण प्राप्त की वह निम्न है
P(c)dc = 4 π[m/2 πkT]3/2 c2e-[mc2/2kt]dc ……………(54)
इस समीकरण को मैक्सवेल ने 1860 में प्राप्त किया था और इसे मैक्सवेल का आण्विक वेगों का वितरण कहा जाता है। व dc वेग के मध्य वाले अणुओं के अंश p(c)dc को dN/N के रूप में भी लिखा जाता है, जहां N गैस अणुओं की कुल संख्या है। अतः उपर्युक्त समीकरण का निम्न रूप हो जाएगा Dn/n0 = 4 π (m/2 Πkt)3/2 e-(mc22KT) C2dc
1/N0 .Dn/dc = 4 π (m/2 Πkt)3/2 e-(mc2/2KT)C2 …………..(55)
जहां c = अणुओं का वेग, dc = वेग में बहुत 1000 अणुओं का वेग थोड़ा-सा परिवर्तन, dn/n0 अणओं की वह भिन्न अथवा अंश (fraction) जिसका वेग तथाc + dc के मध्य
है, एवं प्राकृतिक लॉगरिथ्म का आधार है। यदि [1/N0 Dn/dc x 107] जाए तो विभिन्न तापों पर भिन्न-भिन्न प्रकार के वक्र प्राप्त होते हैं (चित्र 3.161
निष्कर्ष उपयुक्त वक्रो से हम कुछ निम्नांकित सामान्य निष्कर्ष निकाल
- शून्य वेग वाले अणुओं की संख्या भी लगभग शून्य है, ज्यों-ज्यों वेगा तेजी स उस वग वाल अणुओ का अश (Iraction) मा के बढ़ने के साथ उस वेग वाले अणुओं का अंश कम होता जाता है। वेग के इस माओं की संख्या अधिकतम है, प्रायिकतम वेग (most probable velocity) कहते हैं। दो. बाना है। पायिकतम वेग के बाद वेग का मान जितना बढ़ता जाएगा. बही सीअणओं का अंश घटता जाएगा और वेग के अधिकतम मान पर यह संख्या शय अर्थात् बहुत कम व बहुत अधिक वेग वाले अणुओं की संख्या लगभग नग जबकि प्रायिकतम वेग वाले अणुओं की संख्या अधिकतम होती है।
- यदि तीन भिन्न-भिन्न तापों पर खीचे गए वक्रा का हम परस्पर तुलना करें तो पाते है के साथ अणुओं के प्रायिकतम वेग के मान में वृद्धि होती है। a<a <a”
(3) ताप बढ़ने के साथ वक्र की ऊंचाई (height) कम हो जाती है अर्थात् ताप बढ़ने के साथ प्रायिकतम वेग वाले अणुओं की संख्या घटती जाती है। N>N’>N”
(4) ताप बढ़ने के साथ वक्र की चौड़ाई अधिक होती जाती है, इससे निष्कर्ष निकलता है कि वेग में कम अन्तर वाले अणुओं का अंश अधिक हो जाएगा और साथ ही भिन्न-भिन्न अणुओं के वेग और भी बड़े क्षेत्र (range) में भिन्न (different) हो जाएंगे। आनिक बेगों का मैक्सवेत्र
(5) अधिकतम वेग की ओर वक्र का अधिक चौड़ा होना इस बात का संकेत देता है कि प्रायिकतम वेग से अधिक वेग रखने वाले अणुओं की संख्या ताप बढ़ने के साथ बढ़ती जाती है।
tag : derivation of maxwell’s law of distribution of velocities and its experimental verification pdf in hindi
हिंदी माध्यम नोट्स
Class 6
Hindi social science science maths English
Class 7
Hindi social science science maths English
Class 8
Hindi social science science maths English
Class 9
Hindi social science science Maths English
Class 10
Hindi Social science science Maths English
Class 11
Hindi sociology physics physical education maths english economics geography History
chemistry business studies biology accountancy political science
Class 12
Hindi physics physical education maths english economics
chemistry business studies biology accountancy Political science History sociology
English medium Notes
Class 6
Hindi social science science maths English
Class 7
Hindi social science science maths English
Class 8
Hindi social science science maths English
Class 9
Hindi social science science Maths English
Class 10
Hindi Social science science Maths English
Class 11
Hindi physics physical education maths entrepreneurship english economics
chemistry business studies biology accountancy
Class 12
Hindi physics physical education maths entrepreneurship english economics