लॉरेंज बल की परिभाषा क्या है ? lorentz force in hindi लॉरेंज बल का सूत्र लिखिए , किसे कहते है ?
(lorentz force in hindi) लॉरेंज बल की परिभाषा क्या है ? लॉरेंज बल का सूत्र लिखिए , किसे कहते है ?
गतिमान आवेश पर चुम्बकीय बल : लोरेंज बल (force on a moving charge in a magnetic field : lorentz force in hindi) : “जब कोई आवेशित कण किसी चुम्बकीय क्षेत्र में गति करता है तो उस पर गति की दिशा और चुम्बकीय क्षेत्र की दिशा दोनों के लम्बवत एक बल आरोपित होता है जिसे लोरेन्ज बल कहते है। “
माना कि एक धनावेशित कण जिस पर +q आवेश है , B तीव्रता के चुम्बकीय क्षेत्र में क्षेत्र की दिशा के लम्बवत v वेग से चल रहा है। प्रयोगों द्वारा यह देखा गया है कि आवेशित कण एक बल का अनुभव करता है जिसका मान ऐसी दशा में अधिकतम होता है जब आवेशित कण चुम्बकीय क्षेत्र में क्षेत्र के लम्बवत गति करता है। इस अधिकतम बल का परिमाण निम्नलिखित दो बातों पर निर्भर करता है –
- लोरेन्ज बल F का मान कण के आवेश q के अनुक्रमानुपाती होता है अर्थात
F ∝ q
- लोरेन्ज बल आवेशित कण के वेग v के अनुक्रमानुपाती होता है अर्थात
F ∝ v
उक्त दोनों को मिलाने पर
F ∝ qv
F = Bqv अथवा F = qvB . . . . . . . . . . . . . समीकरण-1
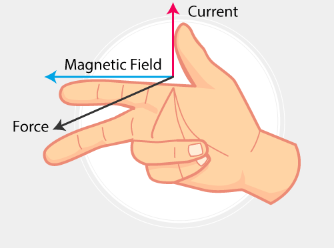
जहाँ B एक नियतांक है जिसे चुम्बकीय प्रेरण (या चुम्बकीय क्षेत्र) कहते है। यह एक सदिश राशि है। लोरेन्ज बल की दिशा फ्लेमिंग के बाएं हाथ के नियम से ज्ञात की जा सकती है। चित्र (a) धनावेशित कण पर लगने वाले बल की दिशा व्यक्त की गयी है। यदि आवेश ऋणात्मक है तो लोरेन्ज बल की दिशा चित्र (a) में प्रदर्शित बल की दिशा के विपरीत होगी क्योंकि फ्लेमिंग के बाएं हाथ के नियम से ऋणावेश के तुल्य धारा धनावेश के कारण तुल्य धारा के विपरीत दिशा में होगी।
यदि आवेशित कण की गति चुम्बकीय क्षेत्र के लम्बवत न होकर उससे θ कोण बना रही हो [चित्र (b)] तो वेग का एक घटक vcosθ चुम्बकीय क्षेत्र (B) के अनुदिश होगा तथा vsinθ क्षेत्र के लम्बवत होगा। अत: लोरेन्ज बल ज्ञात करने के लिए समीकरण (1) में v के स्थान पर vsinθ रखना होगा।
अत: लोरेंज बल
F = qvBsinθ . . . . . . . . . . . . . समीकरण-2
सदिश रूप में इस बल को निम्नलिखित प्रकार व्यक्त किया जाता है –
F = q(v x B) . . . . . . . . . . . . . समीकरण-3
लोरेन्स बल के बारे में निम्नलिखित तथ्य जानने योग्य है –
(1) यदि आवेशित कण का वेग v शून्य हो तो उस पर लगने वाला बल भी शून्य होगा। अत: अत: चुम्बकीय बल केवल गतिमान आवेशित कण पर लगता है जबकि विद्युत बल आवेशित कण पर सदैव कार्य करता है चाहे कण गतिमान अवस्था में हो अथवा विरामावस्था में हो।
(2) यदि θ = 0°C (अर्थात आवेशित कण की गति चुम्बकीय क्षेत्र के अनुदिश हो) या θ = 180°C (अर्थात कण की गति चुम्बकीय क्षेत्र के विपरीत दिशा में हो ) तो sinθ = 0 अत: F = 0 अर्थात कण पर लगने वाला लोरेन्ज बल शून्य होगा। इस स्थिति में कण उसी सरल रेखा में उसी चाल से निकल जायेगा। अत: यह भी कहा जा सकता है कि चुम्बकीय क्षेत्र की दिशा वह दिशा है जिसके अनुदिश गतिमान आवेशित कण पर कोई बल नहीं लगता है।
(3) यदि θ = 90°C (अर्थात आवेशित कण क्षेत्र के लम्बवत गति करे ) तो sinθ = 1
अत: Fmax = qvB
इस बल की दिशा v और B दोनों के लम्बवत होगी जिसे फ्लेमिंग के बाएं हाथ के नियम से ज्ञात करेंगे। यह ध्यान देने योग्य है कि v और F सदैव एक दूसरे के लम्बवत होते है। इसी प्रकार वेक्टर F और B सदैव एक दूसरे के लम्बवत होते है लेकिन v और B के मध्य कुछ भी कोण हो सकता है। यह भी ध्यान देने योग्य है कि चुम्बकीय बल की दिशा चुम्बकीय क्षेत्र के लम्बवत होती है जबकि विद्युत बल की दिशा धनावेश पर वैद्युत क्षेत्र E के अनुदिश और ऋणावेश पर विद्युत बल की दिशा E के विपरीत होती है।
(4) ऋण आवेशित कण पर बल F की दिशा चित्र (a) में प्रदर्शित F की दिशा के विपरीत होगी।
लोरेंज बल का प्रायोगिक प्रदर्शन (experimental demonstration of lorentz force)
चुम्बकीय क्षेत्र में गतिशील आवेश पर लगने वाले लोरेन्ज बल का प्रायोगिक प्रदर्शन कैथोड किरण नलिका द्वारा अग्र प्रकार किया जा सकता है –
कैथोड किरण नालिका की इलेक्ट्रॉन गन से निर्गत इलेक्ट्रॉन पुंज को एक नियंत्रक ग्रिड की सहायता से बारीक किरण पुंज में परिणित कर लेते है। नलिका के दुसरे सिरे पर लगे प्रतिदीप्तिशील पर्दे पर जब यह इलेक्ट्रॉन पुंज टकराता है तो उस स्थान पर एक प्रकाश बिंदु उत्पन्न हो जाता है। इस नलिका को किसी चुम्बकीय क्षेत्र में रखने पर हम देखते है कि प्रकाश पुंज अपनी मूल स्थिति से एक ओर को विक्षेपित हो जाता है। इससे यह सिद्ध होता है कि चुम्बकीय क्षेत्र में गतिशील आवेश पर एक बल कार्य करता है।
चुम्बकीय क्षेत्र B का मात्रक – चुम्बकीय क्षेत्र B की परिभाषा लोरेन्ज बल के आधार पर की जा सकती है। समीकरण -1 से –
F = qvB
B = F/qv
अत: B का मात्रक = F का मात्रक/q का मात्रक x v का मात्रक
= (न्यूटन)/(कुलामxमीटर/सेकंड)
= न्यूटन/मीटर x (कुलाम/सेकंड)
= न्यूटन/मीटरxएम्पियर
= N/m.A = N.A-1m-1
B के इस मात्रक NA-1m-1 को टेस्ला भी कहते है तथा T से व्यक्त करते है अत:
1 NA-1m-1 = 1 T
सूत्र B = F/qv में यदि F = 1 N , q = 1 C , v = 1 ms-1
तो B = 1 NA-1m-1 = 1T
अर्थात यदि 1C आवेश किसी चुम्बकीय क्षेत्र में क्षेत्र के लम्बवत 1 ms-1 के वेग से गति करे तथा आवेश पर 1N का लोरेन्ज बल कार्य करे तो चुम्बकीय क्षेत्र की तीव्रता 1 NA-1m-1 होगी।
टेस्ला चुम्बकीय क्षेत्र का बड़ा मात्रक है अत: चुम्बकीय क्षेत्र को C.G.S. मात्रक गॉस में भी व्यक्त किया जाता है जिसका टेस्ला से निम्नलिखित सम्बन्ध है –
1 टेस्ला = 1 NA-1m-1 = 104 गॉस
चुम्बकीय क्षेत्र का एक अन्य मात्रक वेबर/मीटर2 भी है अत:
1 टेस्ला = 1 NA-1m-1 = 1 वेबर/मीटर2 = 104 गॉस
पृथ्वी का चुम्बकीय क्षेत्र लगभग 0.5 गॉस है। प्रयोगशाला में सामान्य विद्युत चुम्बकों द्वारा एक टेस्ला की कोटि का चुम्बकीय क्षेत्र उत्पन्न किया जाता है। 200 से 400 टेस्ला की कोटि का चुम्बकीय क्षेत्र बहुत अल्प समय के लिए ही उत्पन्न किया जाता है। ऐसा विश्वास किया जाता है कि कुछ आकाशीय तारों में इनसे भी कही प्रबल चुम्बकीय क्षेत्र पाए जाते है , इन तारों को न्यूट्रोन तारे कहते है।
चुम्बकीय क्षेत्र B के मूल मात्रक और विमीय सूत्र –
B का मात्रक = (न्यूटन)/(एम्पियर x मीटर)
= किग्रा मीटर/सेकंड2/(एम्पियर x मीटर)
= किग्रा सेकंड-2 एम्पियर-1
= Kg.S-2.A-1
अत: B का विमीय सूत्र = [M1L0T-2A-1]
प्रश्न 1 : एक इलेक्ट्रॉन 5 x 107 ms-1 के वेग से 1T के चुम्बकीय क्षेत्र की दिशा से 30 डिग्री कोण पर प्रवेश करता है। इलेक्ट्रॉन पर आरोपित बल की गणना कीजिये।
(इलेक्ट्रॉन का आवेश e = 1.6 x 10-19 C)
उत्तर : प्रयुक्त सूत्र F = qvBsinθ
दिया है – V = 5 x 107 ms-1 , B = 1T , θ = 30 degree
q = e = 1.6 x 10-19 C , F = ?
अत: F = qvBsinθ
= 1.6 x 10-19 x 5 x 107 x 1 x sin30
अत: F = 4 x 10-12N